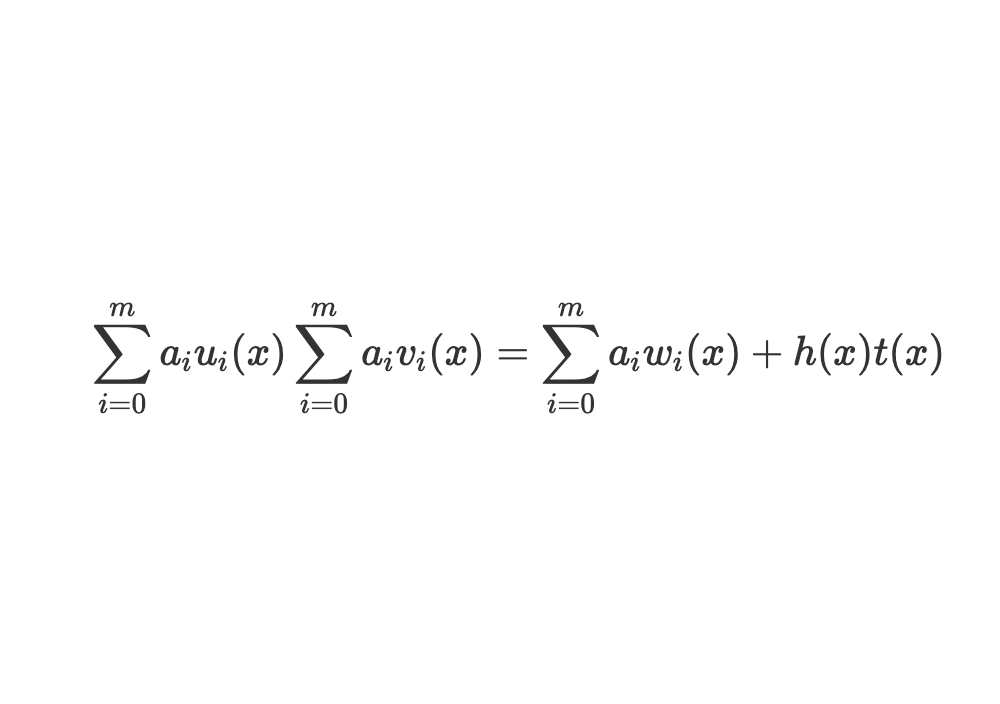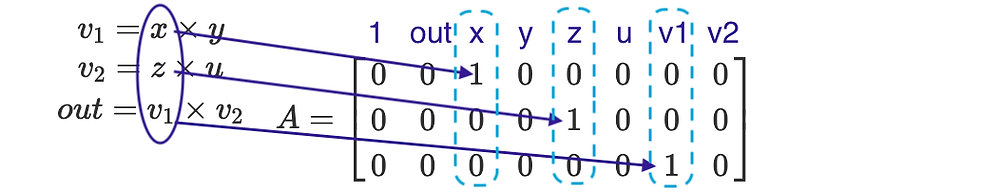The intuition behind elliptic curve digital signatures (ECDSA) This article explains how the ECDSA (Elliptic Curve Digital Signature Algorithm) works as well as why it works. We will incrementally “rediscover” the algorithm from first principles in this tutorial. Prerequisites We assume prior knowledge of Elliptic Curve Arithmetic Elliptic Curve Arithmetic in Finite Fields Digital Signature […]
Trusted Setup A trusted setup is a mechanism ZK-SNARKs use to evaluate a polynomial at a secret value. Observe that a polynomial $f(x)$ can be evaluated by computing the inner product of the coefficients with successive powers of $x$: For example, if $f(x)=3x^3+2x^2+5x+10$, then the coefficients are $[3,2,5,10]$ and we can compute the polynomial as […]
The Schwartz-Zippel Lemma and its application to Zero Knowledge Proofs Nearly all ZK-Proof algorithms rely on the Schwartz-Zippel Lemma to achieve succintness. The Schwartz-Zippel Lemma states that if we are given two polynomials $p(x)$ and $q(x)$ with degree $d_p$ and $d_q$ respectively, and if $p(x) \neq q(x)$, then the number of points where $p(x)$ and […]
Building a Zero Knowledge Proof from an R1CS Given an arithmetic circuit encoded as a Rank 1 Constraint System, it is possible to create a ZK-proof of having a witness, albeit not a succinct one. This article describes how to accomplish that. A zero knowledge proof for a R1CS is accomplished by converting the witness […]
Langrange Interpolation with Python Lagrange interpolation is a technique for computing a polynomial that passes through a set of $n$ points. Interpolating a vector as a polynomial Examples A straight line through two points Consider that if we have two points, they can be interpolated with a line. For example, given $(1, 1)$ and $(2, […]
Polynomial Commitments Via Pedersen Commitments A polynomial commitment is a mechanism by which a prover can convince a verifier a polynomial $p$ has an evaluation $y = p(x)$ at point $x$ without revealing anything about $p$. The sequence is as follows: The prover sends to the verifier a commitment $C$ to the polynomial, “locking in” […]
Homomorphisms A homomorphism between two groups means a structure preserving map between the two groups exists. Suppose we have two algebraic data structures $(A,\square)$ and $(B, \blacksquare)$, where the binary operator of $A$ is $\square$ and the binary operator of $B$ is $\blacksquare$. A homomorphism exists from $A$ to $B$ if and only if there […]
Elementary Group Theory for Programmers This article provides several examples of algebraic groups so that you can build an intuition for them. A group is a set with: a closed binary operator the binary operator is also associative an identity element every element having an inverse We also discussed abelian groups. An abelian group has […]
Abstract Algebra Abstract Algebra is the study of sets that have one or more operators on that set. For our purposes, we only care about binary operators. If we have sets and a binary operator on that set, we can categorize those sets based on how the binary operator behaves, and what elements are allowed […]