Finite Fields for Arithmetic Circuits

This article is the third in a series. We present finite fields in the context of circuits for zero-knowledge proofs. The previous chapters are P vs NP and its Application to Zero Knowledge Proofs and Arithmetic Circuits.

In the previous chapter on arithmetic circuits, we pointed out a limitation that we cannot encode the number 2/3 because it cannot be represented precisely using binary. We also pointed out that we didn’t explicitly have a way to handle overflow.

Both of these issues can be handled seamlessly with a variant of arithmetic, which is popular in general cryptography, called finite fields.

Finite fields

Given a prime number p, we can make a finite field with p elements by taking the set of integers {0, 1, 2, …, p-1} and define addition and multiplication to be done modulo p. We’ll start by limiting ourselves to fields where the number of elements is a prime.

For example, if the prime number p is 7, then the elements in the finite field are {0, 1, 2, 3, 4, 5, 6}. Any number outside this range (≥ p) is always mapped to an “equivalent” number in this range using modulo. The technical word for “equivalent” is congruent.

Modulo calculates the remainder when dividing the number by the prime number. For example, if our modulo is 7, the number 12 is congruent to 5 (12 mod 7 = 5), and the number 14 is congruent to 0. Similarly, when we add two numbers, say 3 + 5, the resulting sum of 8 is congruent to 1 (8 mod 7 = 1). The animation below illustrates this:

In Python, the calculation shown above can be computed as:

p = 7
result = (3 + 5) % p
print(result) # prints 1

In this chapter, whenever we perform calculations, we’ll express our result as a number in the range of 0…(p-1), which is the set of elements in our finite field p. For example, 2 * 5 = 10, which we “simplify” to 3 (modulo 7).

Note how 3 + 5 “overflowed” the limit of 6. In finite fields, overflow is not a bad thing, we define the overflowing behavior to be part of the calculation. In a finite field modulo 7, 5 + 3 is defined to be 1.

How modular arithmetic works

In a typical programming language, we write addition in a finite field as (6 + 1) % 7 == 0, but in mathematical notation, we typically say

0 = 6 + 1 (mod 7)

Or more generally,

c = a + b (mod p)

where a and b are numbers in the finite field, c is the remainder that maps any number ≥ p back in the set {0, 1, …, p - 1}.

Multiplication works similarly by multiplying the numbers together, then taking the modulus:

3 = 4 × 6 (mod 7) = 24 (mod 7) = 3

The multiplication operation above can be visualized in two ways:

Or alternatively:

We refer to a number in a finite field as an “element.”

p and the order of the field

The number we take the modulus with we will call p. In all our examples it is a prime number. In the broader field of mathematics, p might not necessarily be prime, but we will only concern ourselves with cases where p is prime.

Because of this restriction, the order of the field is always equal to p. The order is the number of elements in the field.

For example, if we have p = 5, the elements are {0, 1, 2, 3, 4}. There are 5 elements, so the order of that field is 5.

The p addition identity

Any element plus p is the same element. For example, (3 + 7) mod 7 = 3. Consider the examples in the following animation:

Additive Inverse

Consider that 5 + (-5) = 0.

In mathematics, the additive inverse of a is a number b such at a + b = 0. Generally, we express the additive inverse of a number by placing a negative sign in front. -a is, by definition, the number that when added with a gives 0.

General rules of additive inverses

• Zero is its own additive inverse. 

• Every number has exactly one additive inverse

These additive inverse rules apply to finite fields also. Although we don’t have elements with negative signs like “-5”, some elements can “behave” like negative numbers with respect to each other using the modulo operator.

In regular arithmetic, “-5” is the number that, when added to 5, results in zero. If our finite field is p = 7, then 2 can be considered “-5” because (5 + 2) mod 7 = 0. Similarly, 5 can be considered to be “-2” because they are each other’s additive inverse. To be precise, “-2” is congruent to 5.

To compute the additive inverse of an element, simply compute p - a where a is the element we are trying to find the additive inverse of. For example, to find the additive inverse of 14 modulo 23, we compute 23 - 14 = 9. We can see 14 + 9 (mod 23) = 0. p is congruent to zero, so this is equivalent to computing “-5” as 0 - 5.

Just like real numbers:

• every element in a finite field has exactly one additive inverse

• zero is its own additive inverse.

The general pattern for additive inverses in a finite field is that the elements in the first half of the finite field are the additive inverses of the elements in the second half, as show in the figure below. Zero is the exception since it is its own additive inverse. The numbers connected by the green line are each other’s additive inverse in the field p = 7:

Exercise: Let’s say we pick a p >= 3. Which, if any, non-zero values are their own additive inverse?

Multiplicative inverse

Consider that 5 × (1/5) = 1

The multiplicative inverse for a is a number b such that a * b = 1. Every element except zero has a multiplicative inverse. With “regular numbers,” a multiplicative inverse is 1 / num. For example, the multiplicative inverse of 5 is 1/5, and the multiplicative inverse of 19 is 1/19.

Although we do not have fractional numbers in finite fields, we can still find pairs of numbers that “behave like” fractions when added or multiplied together.

For example, the multiplicative inverse of 4 in the finite field p = 7 is 2, because 4 * 2 = 8, and 8 mod 7 is 1. Thus, 2 “behaves” like 1/4 in the finite field, or to be precise, 1/4 is congruent to 2 (mod 7).

General rules of multiplicative inverses:

• 0 does not have a multiplicative inverse

• 1 is its own multiplicative inverse

• Every number (except 0) has exactly one multiplicative inverse (which could be itself)

• the element of value (p - 1) is its own multiplicative inverse. For example in a finite field of p = 103, 1 and 102 are their own multiplicative inverses. In a finite field of p = 23, 1 and 22 are their own multiplicative inverses (the reason why is explained in the upcoming section). Another example: in the finite field modulo 5, 1 is it’s own inverse, and 4 is its own inverse. 4 * 4 = 16, and 16 mod 5 = 1.

Why element of value p - 1 is its own multiplicative inverse

When we multiply -1 by itself, we get 1. Therefore, -1 is its own multiplicative inverse for real numbers. The element of value (p - 1) is congruent to -1. Therefore, we expect (p - 1) to be its own multiplicative inverse, and indeed that it is the case.

Consider that (p - 1)(p - 1) = p² - 2p + 1. Since p is congruent to 0, then p² - 2p + 1 simplifies to 0^2 - 2*0 + 1 = 1.

Solutions for arithmetic circuits over finite fields

If we consider the following arithmetic circuit over regular numbers, we expect x = -1 to be the only satisfying assignment.

x * x === 1
x + 1 === 0

In a finite field, the satisfying assignment is the element congruent to -1, p - 1.

Computing the multiplicative inverse with Fermat’s Little Theorem

Fermat’s Little Theorem states that

In other words, if you raise a non-zero element to the p, you get that element back. Some examples:

• 3⁵ (mod 5) = 3

• 4⁷ (mod 7) = 4

• 14⁵³ (mod 53) = 14

Now consider if we divide both sides of aᵖ = a (mod p) by a (remember, a ≠ 0):

We can write the result as

This means that aᵖ⁻² (mod p) is the multiplicative inverse of a, since a times aᵖ⁻² is 1.

Some examples:

• The multiplicative inverse of 3 in the finite field p = 7 is 5. 3⁷⁻² = 5 (mod 7)

• The multiplicative inverse of 8 in the finite field p = 11 is 7. 8¹¹⁻² = 7 (mod 11)

The advantage of this approach is we can use the expmod precompile in Ethereum to compute the modular inverse in a smart contract.

In practice, this is not an ideal way to compute multiplicative inverses because raising a number to a large power is computationally expensive. Libraries that compute the multiplicative inverse use more efficient algorithms under the hood. However, when such a library is not a available, Fermat’s Little Theorem can be used.

Computing the multiplicative inverse with Python

Using Python 3.8 or later, we can do pow(a, -1, p) to compute the multiplicative inverse of a in the finite field p. The first argument to pow is the base, the second is the exponent, and the third is the modulus.

Example:

p = 17
print(pow(5, -1, p))
# 7assert 
(5 * 7) % p == 1

Exercise: Find the multiplicative inverse of 3 modulo 5. There are only 5 possibilities, so try all of them and see which ones work.

Exercise: What is the multiplicative inverse of 50 in the finite field p = 51? You do not need Python to compute this, see the principles described in “General rules of multiplicative inverses.”

Exercise: Use Python to compute the multiplicative inverse of 288 in the finite field of p = 311. You can check your work by validating that (288 * answer) % 311 == 1.

The addition of multiplicative inverses is consistent with “regular” addition of fractions

In a finite field of p = 7, the numbers 2 and 4 are multiplicative inverses of each other because (2 * 4) mod 7 = 1. This means that in the finite field p = 7, 4 is congruent to 1/2 and 2 is congruent to 1/4.

We say 4 congruent to 1/2 in the finite field of p = 7 because 2 * (multiplicative_inverse(2)) = 1. The multiplicative inverse of 2 is 4 in this finite field, so we can treat 4 like 1/2.

With real numbers, if we add 1/2 + 1/2, we expect to get 1. The same thing happens in a finite field. Since 4 “behaves like” 1/2, we expect 4 + 4 (mod 7) = 1, and indeed it does.

We are able to encode the number “5/6” in a finite field by thinking of it as the operation 5 * (1/6), or 5 * multiplicative_inverse(6).

Consider that 1/2 + 1/3 = 5/6. If our finite field is p = 7, then 1/2 is the multiplicative inverse of 2, 1/3 is the multiplicative inverse of 3, and 5/6 is 5 times the multiplicative inverse of 6:

p = 7
one_half = pow(2, -1, p)
one_third = pow(3, -1, p)
five_over_six = (pow(6, -1, p) * 5) % p

assert (one_half + one_third) % p == five_over_six
# True

The general way to compute a “fraction” in a finite field is the numerator times the multiplicative inverse of the denominator, modulo p:

def compute_field_element_from_fraction(num, den, p):
    inv_den = pow(den, -1, p)
    return (num * inv_den) % p

It is not possible to do this when the denominator is a multiple of p. For example, 1/7 cannot be represented in the finite field p = 7 because pow(7, -1, 7) has no solution. The modulo is taking the remainder after division, and the remainder of 7/7 is zero, or more generally, 7/d is zero when d is a multiple of 7. The multiplicative inverse means we can multiply a number and its inverse together to get 1, but if one of the numbers is zero, there is nothing we can multiply by zero to get 1.

Exercise: run pow(7, -1, 7) in Python. You should see an exception get thrown, ValueError: base is not invertible for the given modulus.

7 mod 7 equals zero. There is nothing we can multiply by zero to get 1.

Finite field “division” does not suffer from precision loss

If we divide 1 / 3 in most programming languages, we will suffer from precision loss because 0.3̅ is not representable in binary.

However, 1 / 3 in a finite field is simply the multiplicative inverse of 3.

This means the arithmetic circuit

x + y + z === 1;
x === y;
y === z;

has an exact solution when done in a finite field. This would not be possible to do reliably if we used fixed point or floating point numbers as the data types for our arithmetic circuits (consider that adding 0.33333 + 0.33333 + 0.33333 will result in 0.99999 rather than 1).

The following implementation in Python illustrates the circuit:

p = 11

# x, y, z have value 1/3
x = pow(3, -1, 11)
y = pow(3, -1, 11)
z = pow(3, -1, 11)

assert x == y;
assert y == z;
assert (x + y + z) % p == 1

Finite field elements do not have a traditional notion of “even” or “odd”

We say a number is “even” if it can be divided by two with no remainder.

In a finite field, any element can be divided by two with no remainder.

That is, “dividing by two” is really multiplying by the multiplicative inverse of 2, and that will always result in another field element without “remainder.”

However, if we have a binary representation of the field element, then we can check if the element is even or odd if it were cast to an integer. If the least significant bit is 1, then the number is odd (if interpreted as an integer, not a finite field element).

Finite field library in Python

Because it can be a bit tedious to keep writing pow and % p in Python, the reader may wish to use the galois library instead (finite fields are sometimes called Galois fields, pronounced “Gal-wah”). It can be installed with python3 -m pip install galois.

Below, we translate the addition of fractions code from the above section (1/2 + 1/3 = 1/6) to use the galois library instead. The library overwrites the math operators to work in a finite field:

import galois
GF7 = galois.GF(7) # GF7 is a class that wraps 7

one_half = GF7(1) / GF7(2)
one_third = GF7(1) / GF7(3)
five_over_six = GF7(5) / GF7(6)

assert one_half + one_third == five_over_six

The operation 1 / GF(a) computes the multiplicative inverse of a.

The galois library can compute the additive inverse by adding a negative sign in front:

negative_two = -GF(2)
assert negative_two + GF(2) == 0

The multiplication of fractions is also consistent

Let’s use finite field p = 11 for this example.

With regular numbers we know that 1/3 * 1/2 = 1/6.

Let’s do this same operation in a finite field:

import galois
GF = galois.GF(11)

one_third = GF(1) / GF(3)
one_half = GF(1) / GF(2)
one_sixth = GF(1) / GF(6)

assert one_third * one_half == one_sixth

Exercise: check that 3/4 * 1/2 = 3/8 in the finite field p = 17.

a × b ≠ 0 for all nonzero a, b

No two elements can be multiplied together to obtain zero in a finite field unless one of the elements is zero itself. This is also true of regular numbers.

To understand this, consider the finite field p = 7. To multiply two numbers together and get 0 as a result, then one of the terms a needs to be a multiple of 7, so that a (mod 7) is zero. However, if we exclude zero, none of the remaining elements {1, 2, 3, 4, 5, 6} are a multiple of 7, so this cannot happen.

We will refer to this fact frequently when we design arithmetic circuit. For example, if we know

x₁ * x₂ * ... * xₙ ≠ 0 

Then we can be certain all of variables x₁, x₂, xₙ are non-zero — even if we don’t know their values.

Here’s how we can use this trick for a realistic arithmetic circuit. Suppose we have signals x₁, x₂, x₃. We wish to constrain at least one of these signals to have the value 8 without specifying which one does. First we compute the additive inverse of 8 a_inv(8) for our field. Then we do:

(x₁ + a_inv(8))(x₂ + a_inv(8))(x₃ + a_inv(8)) === 0

This could be written as

(x₁ - 8)(x₂ - 8)(x₃ - 8) === 0

with the understanding that -8 is the additive inverse of 8 for our finite field.

As long of one of the signals has the value 8, then that term will be zero and the whole expression will multiply to zero. This trick relies on two facts:

• If all of the terms are non-zero, there is no way for the expression to evaluate to zero

• The additive inverse of 8 is unique, and 8 is the uniquely additive inverse for the additive inverse of 8. In other words, there is no value except 8 that results in 8 + inv(8) being zero.

Therefore, the arithmetic circuit (x₁ + a_inv(8))(x₂ + a_inv(8))(x₃ + a_inv(8)) === 0 states that at least one of x₁, x₂, xₙ has the value 8.

Finite field operations are associative, commutative, and distributive

Just like with regular math, in finite fields, the associative, commutative, and distributive properties hold, i.e.

associative

(a + b) + c = a + (b + c) (mod p)

commutative addition

(a + b) = (b + a) (mod p)

commutative multiplication

ab = ba (mod p)

distributive

a(b + c) = ab + ac (mod p)

Modular square roots

In “regular math,” perfect square numbers have integer square roots. For example, 25 has a square root of 5, 49 has a square root of 7, and so on.

Elements in a finite field do not need to be perfect squares to have a square root

Consider that 5 × 5 (mod 11) = 3. This means that the square root of 3 is 5, modulo 11. Because of how finite fields wrap around, finite field elements do not have to be perfect squares to have a square root.

Just like regular square roots, which have two solutions: a positive and negative one, modular square roots in a finite field also have two solutions. The exception is the element 0, which only has 0 as its square root.

In the finite field modulo 11, the following elements have square roots:

Element	1st Square Root	2nd Square Root
0	0	n/a
1	1	10
3	5	6
4	2	9
5	4	7
9	3	8

Exercise: Verify the claimed square roots in the table are correct in the finite field modulo 11.

Observe that the second square root is always the additive inverse of the first square root, just like real numbers.

For example:

• In regular math, the square roots of 9 are 3 and -3, where both are additive inverses of each other.

• In a finite field of p = 11, the square roots of 9 are 3 and 8. 8 is the additive inverse of 3 because 8 + 3 (mod 11) is 0, just as 3 is the additive inverse of -3.

The elements 2, 6, 7, 8, and 10 do not have modular square roots in the finite field p = 11. This can be discovered by squaring every element from 0 to 10 inclusive, and seeing that 2, 6, 7, 8, and 10 are never produced.

numbers_with_roots = set()
p = 11
for i in range(0, p):
    numbers_with_roots.add(i * i % p)

print("numbers_with_roots:", numbers_with_roots)
# numbers_with_roots: {0, 1, 3, 4, 5, 9}

Note that 3 is not a perfect square, but it does have a square root in this finite field.

Computing the modular square root

The modular square root can be computed in Python with the libnum library. Below, we compute the square root of 5 modulo 11. The third argument to the functions has_sqrtmod_prime_power and sqrtmod_prime_power can be set to 1 for our purposes.

# install libnum with `python -m pip install libnum`

from libnum import has_sqrtmod_prime_power, sqrtmod_prime_power

has_sqrtmod_prime_power(5, 11, 1) # True
list(sqrtmod_prime_power(5, 11, 1)) # [4, 7]

# square roots generally have two solutions. 4 and 7 are the square roots of 5 (mod 11)

When p can be written as 4k + 3 where k is an integer, then the modular square root can be computed as follows:

def mod_sqrt(x, p):
        assert (p - 3) % 4 == 0, "prime not 4k + 3"
        exponent = (p + 1) // 4
        return pow(x, exponent, p) # x ^ e % p

The function above returns one of the square roots of of x modulo p. The other square root can be computed by calculating the additive inverse of the value returned. If the prime number is not of the form 4k + 3 then the Tonelli-Shanks algorithm must be used to compute the modular square root (which the libnum library above implements).

The implication for this is that the arithmetic circuit x * x === y may have two solutions. For example, in a finite field p = 11, it might seem that the arithmetic circuit x * x === 4 only admits the value 2 because -2 is not a finite field element. However, that assumption is very wrong! The assignment x = 9, which is congruent to -2, also satisfies the circuit.

Exercise: Use the code snippet above to compute the modular square root of 5 in the finite field of p = 23. The code will only give you one of the answers. How can you compute the other?

Linear systems of equations in finite fields

As noted in the previous chapter, an arithmetic circuit is essentially a system of equations. Linear systems of equations in a finite field share a lot of properties as a linear system of equation over regular numbers. However, there are some differences which may initially be unexpected. Since arithmetic circuits are computed over finite fields, we must understand where these surprising deviations may be.

A linear system of equations is a collection of straight-line equations with a set of unknowns (variables) that we try to solve together. To find the unique solution to a system of linear equations, we must find a numerical value for each variable that will satisfy all equations in the system simultaneously.

Linear systems of equations with real numbers either have:

1) No solution: which means the two equations represent lines that are parallel in two dimensions, or never cross in three dimensions or higher

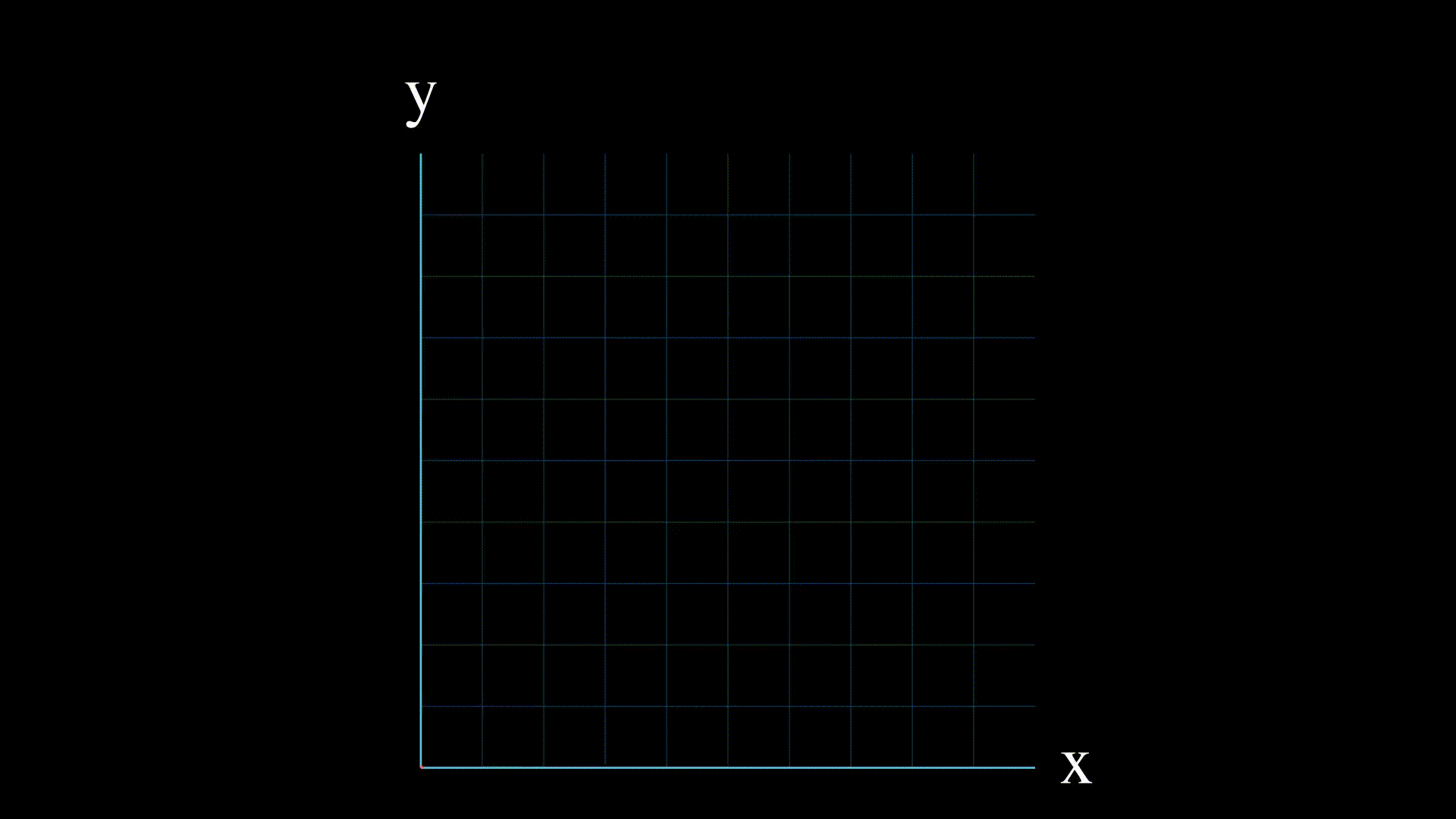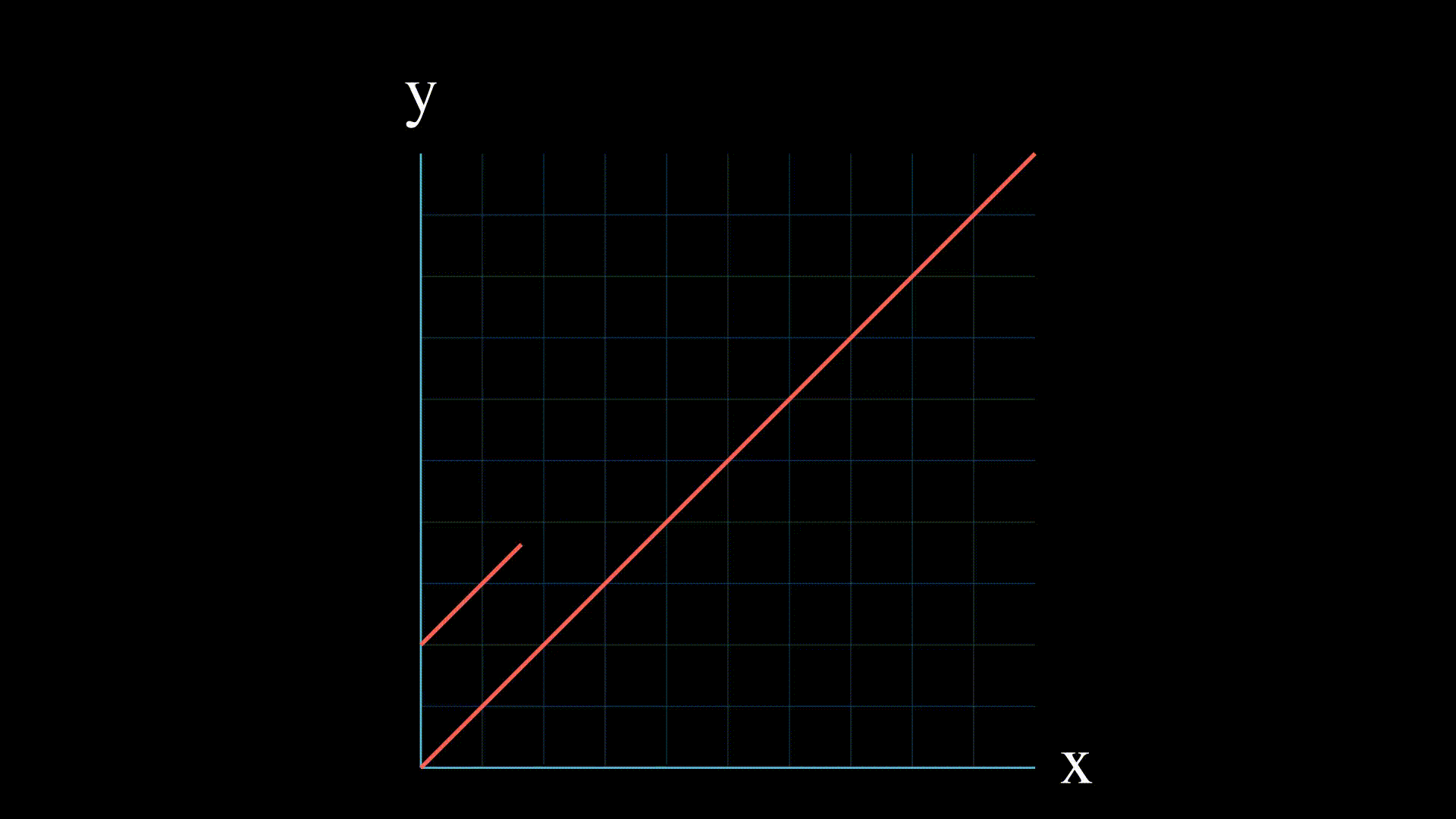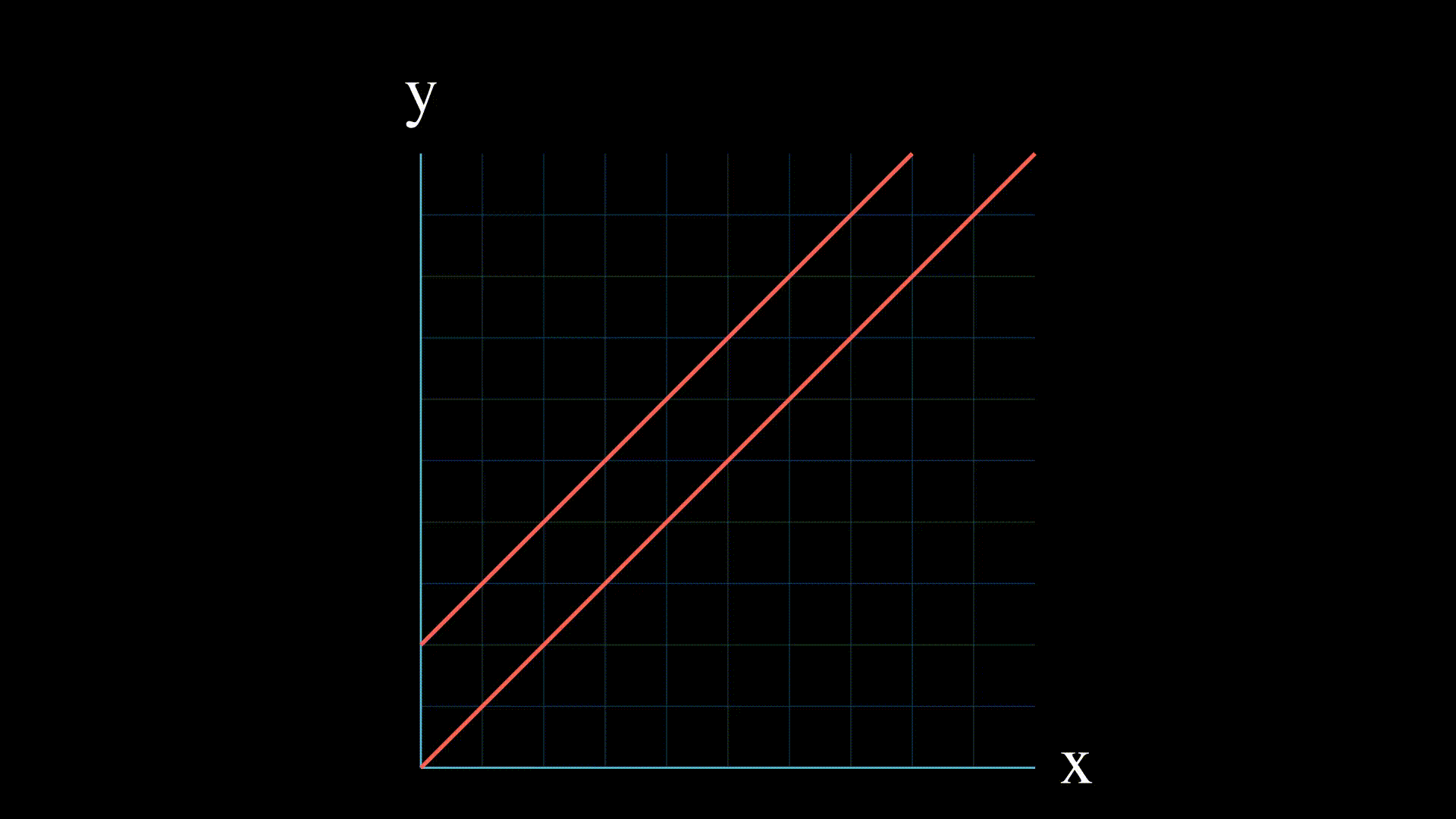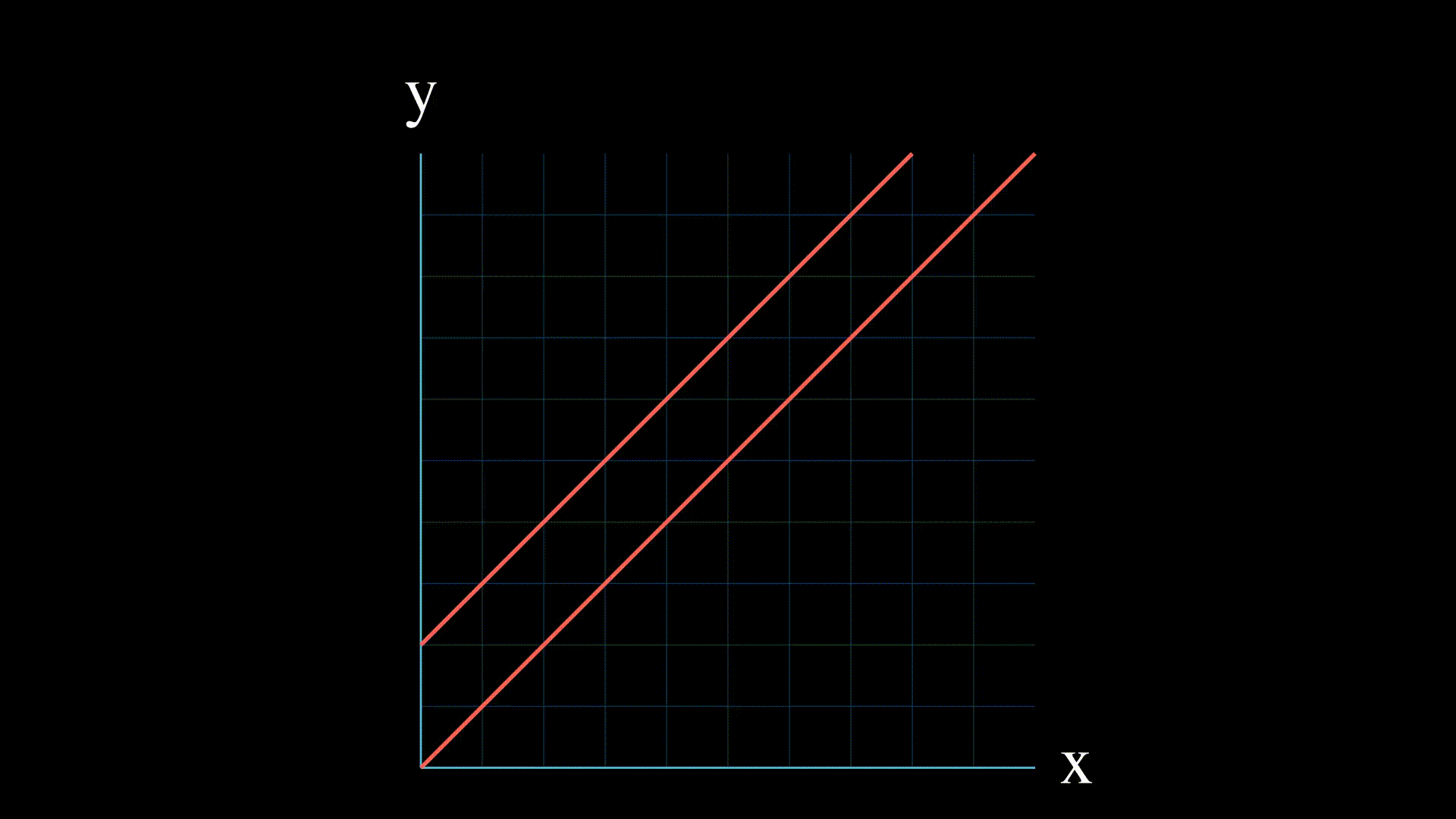
2) One solution which means the lines intersect at one point

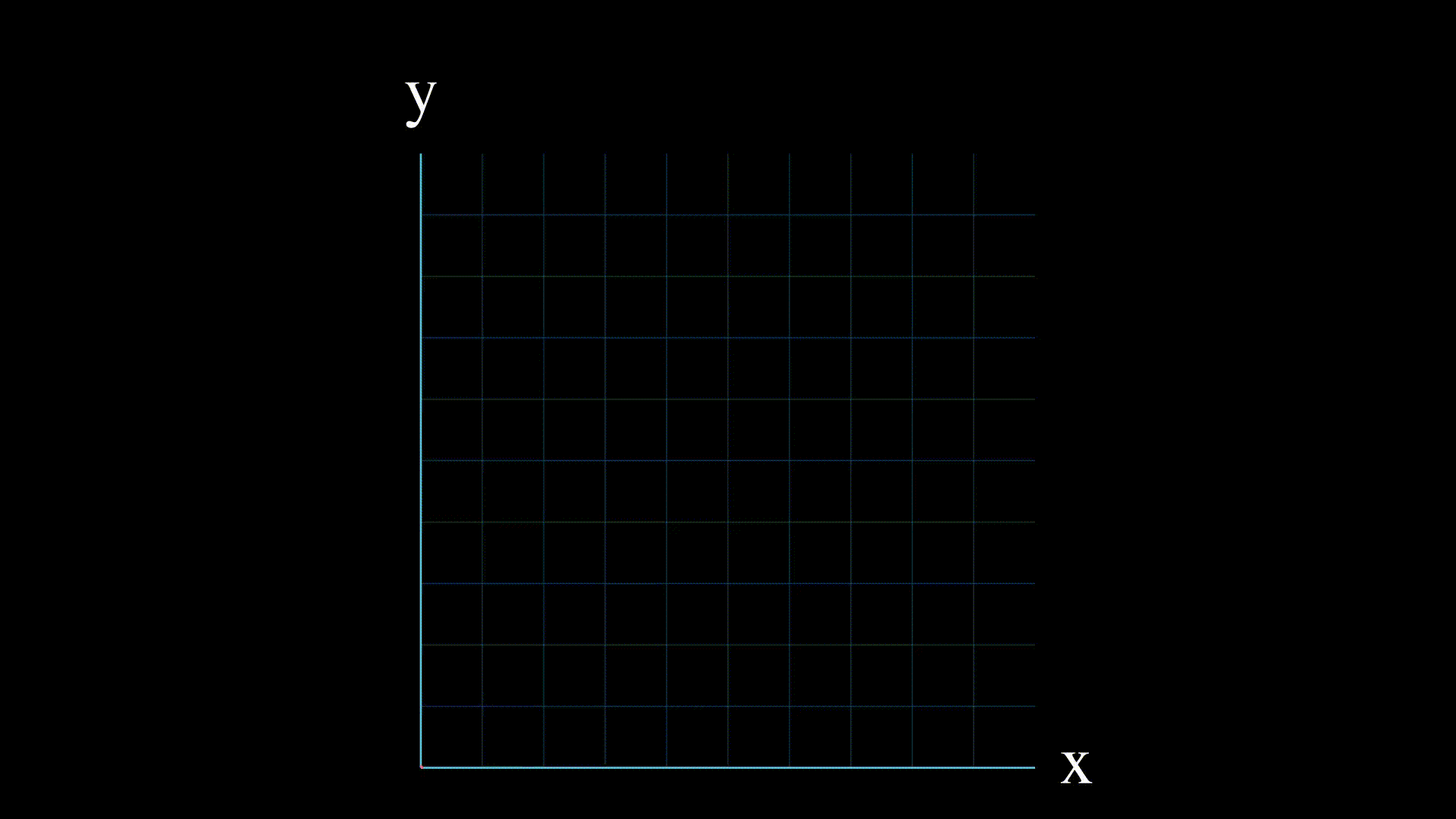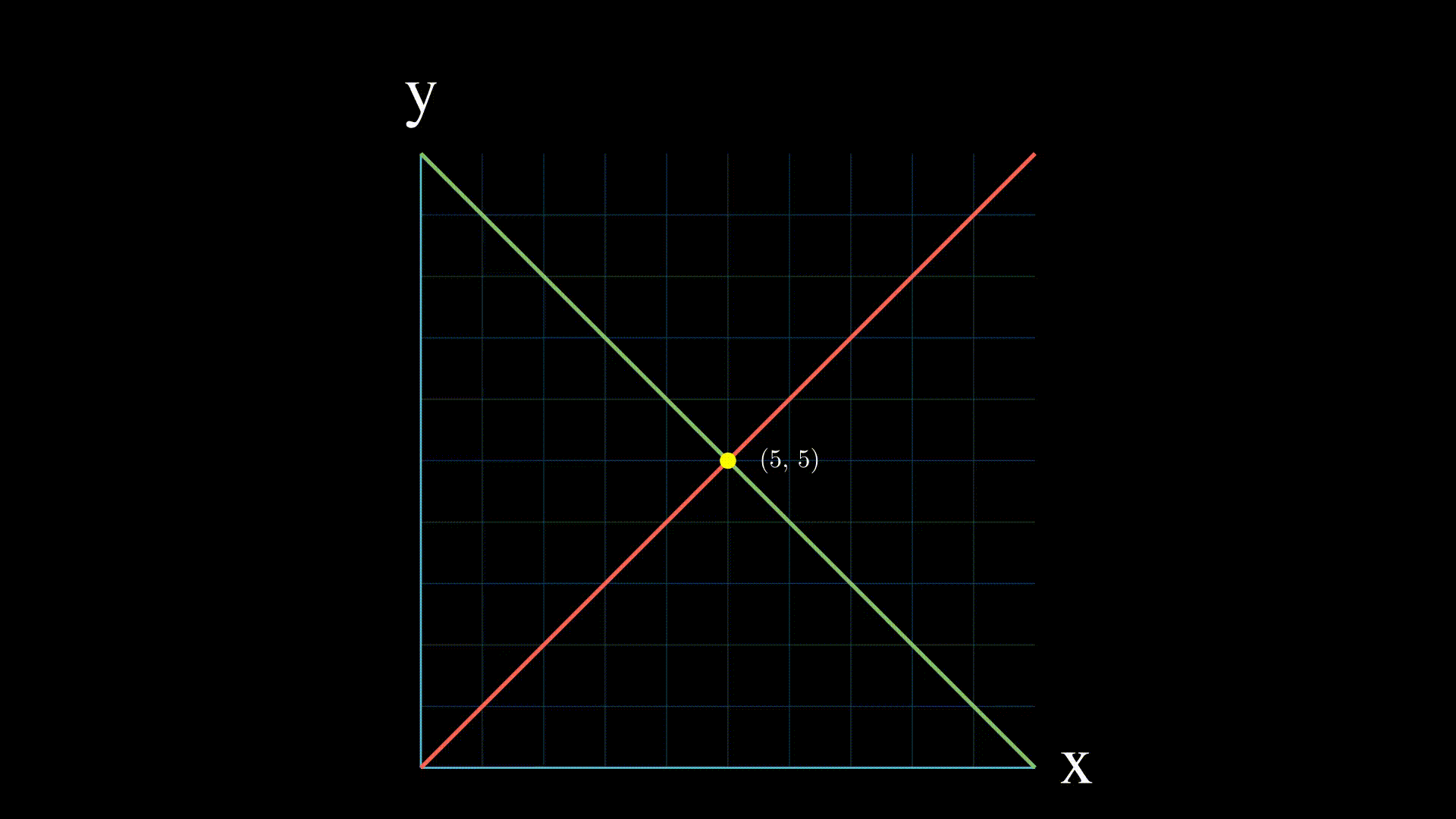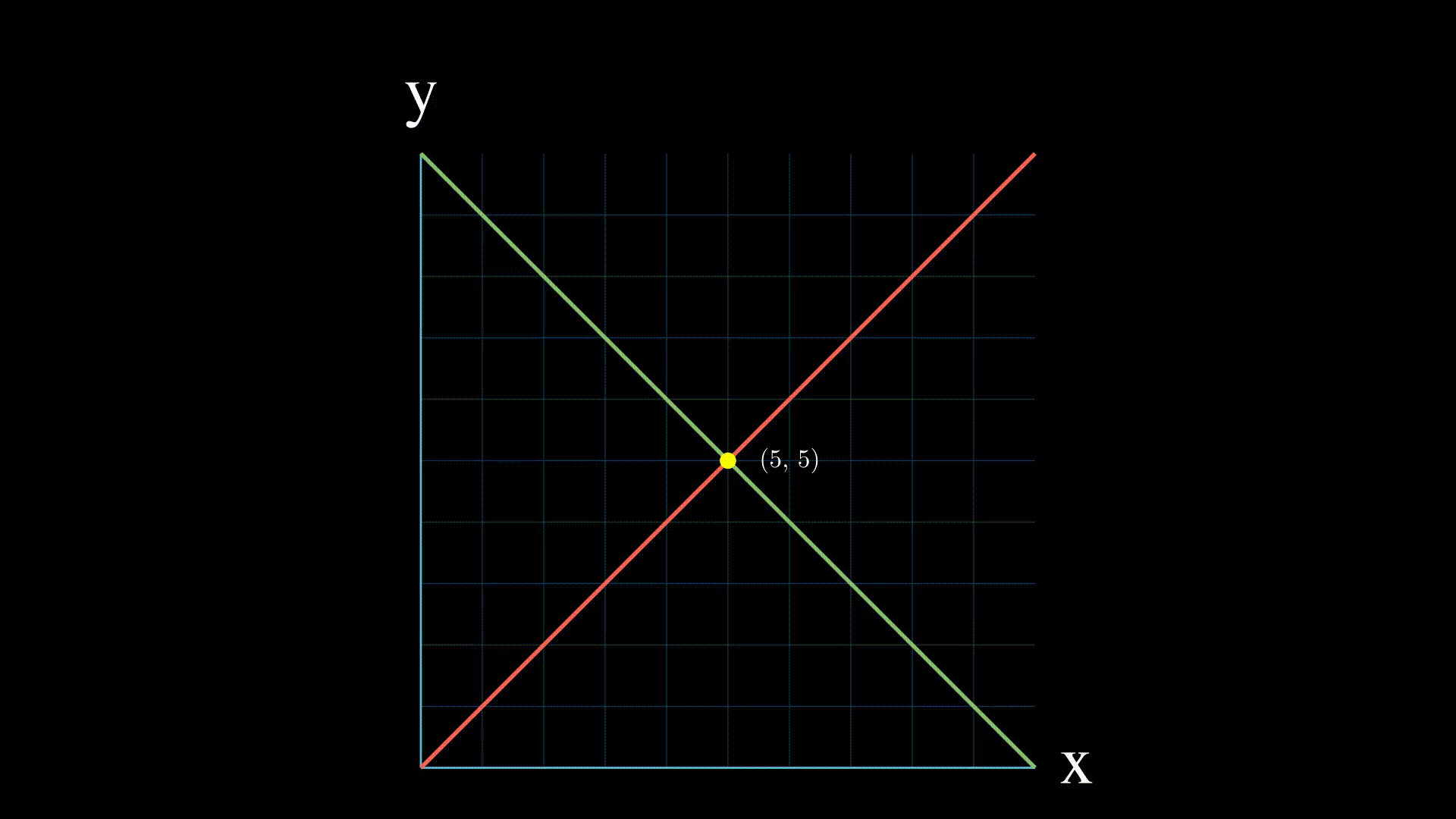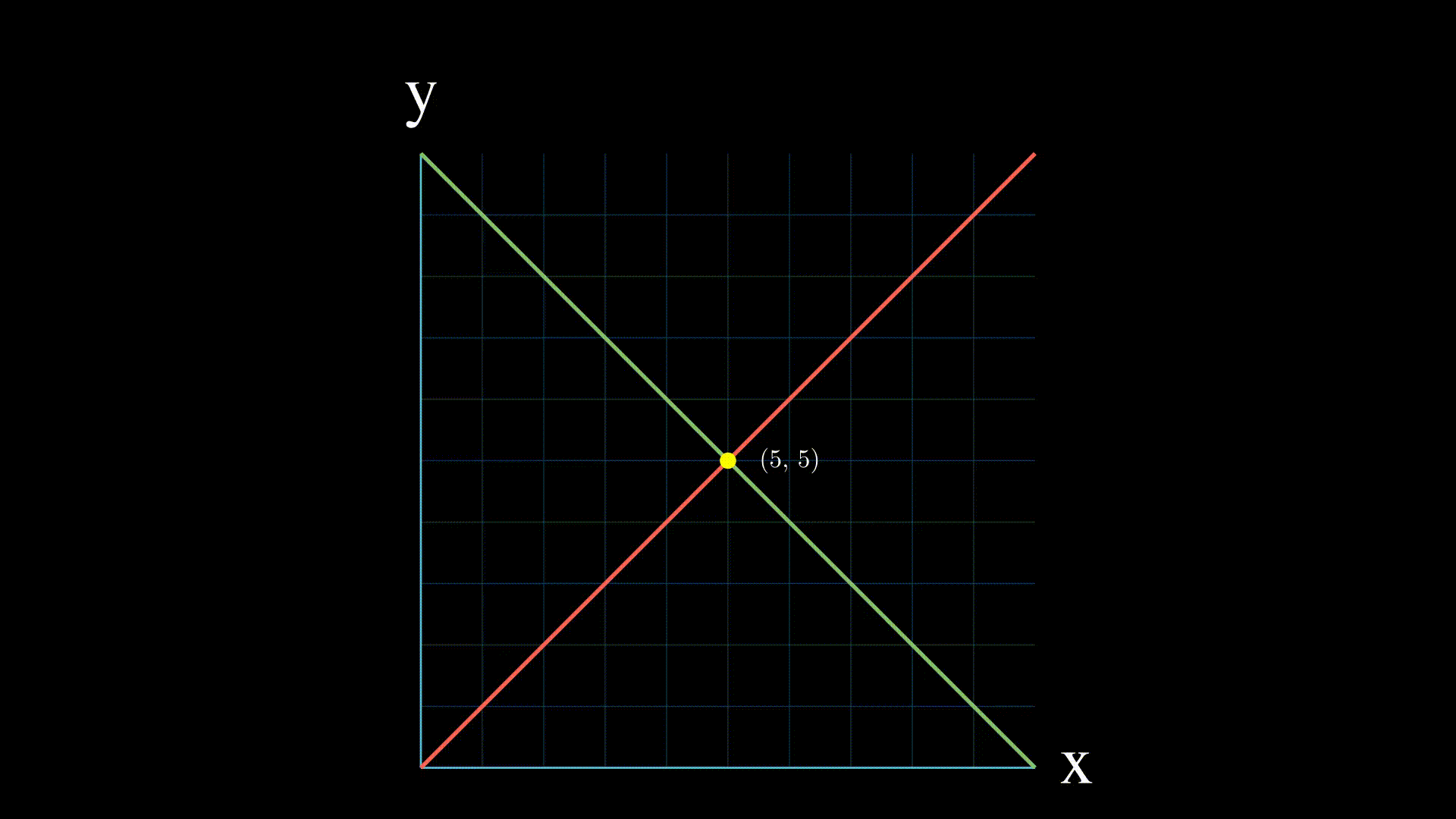
3) Infinite solutions: if the two equations represent the same line, then there are infinitely many points of intersection, and the linear system of equations has an infinite number of solutions.

Finite field systems of equations also have

1. no solution

2. one solution

3. or p many solutions, i.e. as many solutions as the order of the field

However, just because a linear system of equations over real numbers has zero, one, or infinite solutions it does not imply that the same linear system of equations over a finite field will also have zero, one or, p many solutions.

The reason we emphasize this is because we use arithmetic circuits and an assignment to the signals to encode our solution to a problem in NP. However, because arithmetic circuits are encoded with finite fields, we may end up encoding the problem in a way that does not capture the behavior of the equations we are trying to model.

The following three examples show how the behavior of a system of equations can change when done over a finite field.

Example 1: A system of equations with one solution over regular numbers may have p many solutions in a finite field

For example, we plot:

It has one solution: (1, 0) for real numbers, but over the finite field p = 11, it has 11 solutions: (0, 6), (1, 0), (2, 5), (3, 10), (4, 4), (5, 9), (6, 3), (7, 8), (8, 2), (9, 7), (10, 1).

Don’t assume that a system of equations (arithmetic circuit) that has a single solution in real numbers has a single solution in a finite field!

Below we plot the solutions to the systems of equation over the finite fields to illustrate both equations “intersect everywhere,” that is, have the same set of points that satisfy both equations:

This might seem extremely counterintuitive — let’s see how it happens. If we solve the original equations:

for y we get:

“1/2” is the multiplicative inverse of 2. In a finite field of p = 11, 6 is the mutiplicative inverse of 2, i.e. 2 * 6 (mod 11) = 1. Therefore, x + 2y = 1 and 6x + y = 6 are actually the same equation in finite field p = 11. That is, the equation y = 1/2 - 1/2x when encoded in a finite field is y = inv(2) - inv(2)x which is y = 6 - 6x — the same as the other equation in the system.

Example 2: A system of equations with one solution over regular numbers may have zero solutions in a finite field

Also counterintuitively, a system of equations with a single solution over real numbers may have no solution in a finite field:

Clearly, this system of equations has an intersection point, but over a finite field it has no solution.

Below we show the plot of the two equations in a finite field:

Exercise: Write code to bruteforce every combination of (x, y) over x = 0..10, y = 0..10 to verify the above system has no solution over the finite field of p = 11.

Why does this system of equations have no solution in finite field p = 11?

If we solve

for real numbers, we get the solutions

The fractions above do not have a congruent element in the finite field p = 11.

Recall that dividing by a number is equivalent to multiplying by its multiplicative inverse. Also, recall the field order (in this case 11) won’t have a multiplicative inverse, because the field order is congruent to 0.

The multiplicative inverse of a is the value b such that a * b = 1. However, if a = 0 (or any value congruent to it) then there is no solution for b. So, the expressions we wrote for the solutions in the real numbers can’t be translated into elements of our finite field.

Therefore the solutions (x, y) above are not part of the finite field. Hence, in a finite field p = 11, x + 2x = 1 and 7x + 3y = 2 are parallel lines.

To see this from another angle, we could solve the equations for y and get:

We saw in the previous section that 6 is the multiplicative inverse of 2, so the first equation has a “slope” of 6 in the the finite field. In the second equation, we compute the slope by computing 7 times the multiplicative inverse of 3: (7 * pow(3, -1, 11)) % 11 = 6 . We now show that their slopes are the same in a finite field.

The slope is the coefficient of x in the form y = c + bx. For the two equations above, the first slope is -1/2 and the second slope is -7/3. If we convert both of these fractions to an element in the finite field of p = 11, we get the same value of 5:

import galois
GF11 = galois.GF(11)

negative_1 = -GF11(1)
negative_7 = -GF11(7)

slope1 = GF11(negative_1) / GF11(2)
slope2 = GF11(negative_7) / GF11(3)

assert slope1 == slope2 # 5 == 5

The implication of this fact for the arithmetic circuit:

x + 2 * y === 1
7 * x + 3 * y === 2

is that the arithmetic circuit does not have a satisfying assignment in a finite field p = 11.

Example 3: A system of equations with zero solutions over regular numbers may have p solutions in a finite field

The following two formulas plot lines that are parallel and hence have no solution over reals:

However, over the finite field p=11 , it has 11 solutions: (0, 7), (1, 1), (2, 6), (3, 0), (4, 5), (5, 10), (6, 4), (7, 9), (8, 3), (9, 8), (10, 2). Those solutions are plotted below:

Exercise: Convert the two equations to their finite field representation and see they are the same.

Suppose we encoded this system of equations as an arithmetic circuit:

x + 2 * y === 3
4 * x + 8 * y === 1

For the finite field we are using, our constraints are redundant even though they “look different.” That is, two different looking constraints actually constrain x and y to have the same values.

Polynomials in finite fields

In the chapter on Arithmetic circuits, we used the polynomial x(x - 1) === 0 to enforce that x can only be 0 or 1. This could be written as a polynomial equation. To do so, we fully expand our expression until it’s expressed as separate powers of x, each multiplied by a coefficient. In this case: x² - x === 0.

That assumption that the polynomial x² - x === 0 only has solutions 0 or 1 in a finite field (as well as with real numbers) is sound in this case. However, in general, one should not assume that the roots of a polynomial over real numbers has the same roots in a finite field. We will show some counterexamples later.

Nevertheless, polynomials in finite fields share a lot of properties with polynomials over real numbers:

• A polynomial of degree d has at most d roots. The roots of a polynomial p(x) are the values r such that p(r) = 0.

• If we add two polynomials p1 and p2, the degree of p1 + p2 will be at most max(deg(p1), deg(p2)). It’s possible for the degree of p1 + p2 to be less than max(deg(p1), deg(p2)). For example, p1=x³ + 5x + 7 and p2 = -x³,

• Adding polynomials in a finite field follows associative, commutative, and distributive laws.

• If we multiply two polynomials p1 and p2, the roots of the product will be the union of the roots of  p1 and p2.

Let’s plot y = x² (mod 17) as an example.

The domain of x are the elements of the finite field, and the output (range) must be a member of the finite field as well. That is, note how all the x and y values lie in the interval of [0,16]. A polynomial over a finite field can only have x and y values less than p.

The equivalent of y = -x² in finite field p = 17 is y = 16x² (mod 17) since 16 is the additive inverse of 1 in that finite field.

Polynomials that do not have roots in real numbers may have roots in a finite field

Just like our examples above with linear systems of equations, one should not assume that a polynomial with certain roots in real numbers has the same roots in a finite field.

Below, we plot y = x² + 1 in the finite field p = 17. In real numbers, y = x² + 1 has no real roots. But in a finite field, it has two roots at 4 and 13, marked in red dots below:

Let’s now explain why y = x² + 1 does not have roots in real numbers but does have roots in the finite field p = 17. In the finite field p = 17, 17 is congruent zero. So if we plug a value into x such that x² + 1 becomes 17, then the polynomial will output zero, not 17. We can solvex² + 1 = 17 for x² = 17 - 1 = 16. In a finite field of p = 17, x² = 16 has solutions 4 and 13. Therefore, y = x² + 1 has roots 4 and 13 in the finite field p = 17.

Polynomials with real roots may have no roots in a finite field

Consider the polynomial y = x² − 5. We can see it has roots at √5 and -√5. However, if we plot it over a finite field modulo 17, we can see it never crosses the x-axis:

There are no roots is because √5 cannot be represented in a finite field modulo 17. However, in the finite field p = 11, then there would be two roots because 5 has a modular square roots in the finite field of p = 11.

Limitations in arithmetic circuits for ZK Proofs

If we wish to write an arithmetic circuit to show “I know the root of the polynomial y = x² − 5" using an arithmetic circuit over a finite field, then we may run into the issue of not being able to encode √5. That is, over real numbers, y = x² − 5 has a root of √5, but this cannot be expressed in some finite fields. Depending on p, the arithmetic circuit x² === 5 may have no satisfying witness.

Polynomials in finite fields with Python

When experimenting with arithmetic circuits, it is sometimes helpful to write Python code to simulate them. When our arithmetic circuit has a polynomial form, we can use the galois library from earlier to test its behavior. The following code examples illustrate how to use this library for working with polynomials.

Adding polynomials in a finite field

In the code below, we define two polynomials: p1 = x² + 2x + 102 and p2 = x² + x + 1and then symbolically add them together to produce 2x² + 3x. Note that the constant coefficient terms add up to zero in the finite field p = 103.

import galois
GF103 = galois.GF(103) # p = 103

# we define a polynomial x^2 + 2x + 102 mod 103
p1 = galois.Poly([1,2,102], GF103)

print(p1)
# x^2 + 2x + 102

# we define a polynomial x^2 + x + 1 mod 103
p2 = galois.Poly([1,1,1], GF103)

print(p1 + p2)
# 2x^2 + 3x

The galois library is intelligent enough to interpret negative integers as additive inverses, as the code below demonstrates:

import galois
GF103 = galois.GF(103) # p = 13

# We can input "-1" as a coefficient, and that will
# automatically be calculated as `p - 1`
# -1 becomes 102 in a field p = 103
p3 = galois.Poly([-1, 1], GF103)
p4 = galois.Poly([-1, 2], GF103)

print(p3)
# 102x + 1
print(p4)
# 102x + 2

Multiplying polynomials in a finite field

We can multiply polynomials together:

print(p3 * p4)
# x^2 + 100x + 2

Note that p3 and p4 are degree 1 polynomials and there product is a degree 2 polynomial.

Finding the roots of polynomials in a finite field

Finding roots of polynomials over finite fields is a separate topic (see the Wikipedia page for algorithms on factorizing polynomials over finite fields). The galois library can calculate the roots with the roots function. This may be handy for verifying arithmetic constraints in polynomial form actually create the intended constraints.

print((p3 * p4).roots())
# [1, 2]

galois library gotchas

The library silently takes the floor of floating point numbers passed as coefficients:

# The galois library will silently convert
# floats into a integer
galois.Poly([2.5], GF103)
# Poly(2, GF(103))

The library will revert if passed a number greater than or equal to p:

# The follow code fails because we cannot
# have coefficients the order of the field or higher
galois.Poly([103], GF103)
# ValueError: GF(103) arrays must have elements in `0 <= x < 103`, not [103].

Learn more with RareSkills

See our ZK Book to learn more about Zero Knowledge Proofs

Practice problems

In the problems below, use a finite field p of 21888242871839275222246405745257275088548364400416034343698204186575808495617. Beware that the galois library takes a while to initialize a GF object, galois.GF(p), of this size.

1. A dev creates an arithmetic circuit x * y * z === 0 and x + y + z === 0 with the intent of constraining all the signals to be zero. Find a counter example to this where the constraints are satisfied, but not all of x, y, and z are 0.

2. A dev creates a circuit with the polynomial x² + 2x + 3 === 11 and proves that 2 is a solution. What is the other solution? Hint: write the circuit as x² + 2x - 8 === 0 then factor the polynomial by hand to find the roots. Finally, compute the congruent element of the roots in the finite field to find the other solution.