In early chapters, we introduced the concept of ticks, which discretize the price curve. A tick is a price defined by the formula , where is named tick index.
Tick indexes are integers within the range , resulting in 1,774,545 ticks along the price curve, from to .
Ticks are points on the curve where liquidity may change. For example, a liquidity provider can add liquidity between two ticks but cannot do so between two arbitrary points that are not ticks.
What we will see in this chapter is that not all of these 1,774,545 ticks can be used in a pool, and the specific ticks that can be used depend on a choice made at the time of creating the pool.
Tick spacing
Each pool defines a value called tick spacing, which determines the distance between two consecutive allowed ticks.
For instance, if the tick spacing of the pool is set to 10, only tick indexes that are multiples of 10 are usable, such as -20, -10, 0, 10, 20, etc. If the tick spacing is set to 60, only multiples of 60 are allowed, such as -120, -60, 0, 60, 120, etc, as illustrated in the figure below. In both scenarios, a tick such as 55 cannot be used as a boundary for providing liquidity.
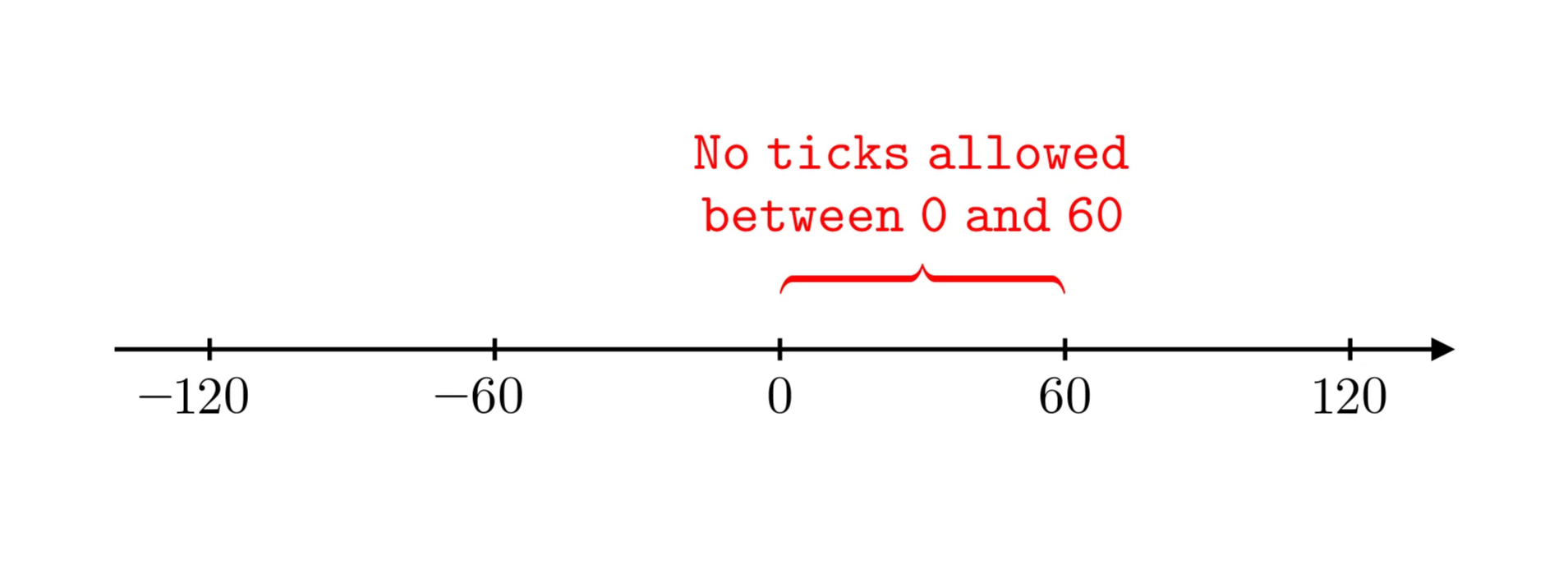
The variable that defines tick spacing in a pool is named tickSpacing and is set at the time of pool creation. In fact, tickSpacing is linked to the pool fee, with each fee tier determining a corresponding tick spacing.
The relationship between volatility, fee tier and tick spacing
Tick spacing and volatility
Uniswap V3 supports different tick spacings to account for the varying volatility of asset pairs. Crossing a tick in a swap incurs a gas cost, so ticks should be crossed as infrequently as possible during a typical trade.
More volatile pairs benefit from wider tick spacing to reduce excessive tick crossings. However, if the spacing is too wide, liquidity providers cannot precisely position their liquidity around the price regions where they expect the pair’s market value to be.
See the animation below, where we present two cases. In the first case, involving a highly volatile pair, the price can vary significantly. So, if we want to try to limit swaps to crossing only two allowed ticks, the distance between allowed ticks must be large. In the second case, involving a more stable pair, the tick spacing can be smaller.
Volatility and fees
Also, consider the risk of impermanent loss for liquidity providers. Highly volatile assets tend to cause higher impermanent loss, while more stable assets tend to cause less impermanent loss. For instance, a stablecoin pair has virtually no risk of impermanent loss, while a memecoin pair carries an extremely high risk.
Thus, LPs will demand higher fees to compensate for impermanent loss when providing liquidity for highly volatile assets. Similarly, traders can tolerate higher fees on volatile assets since the potential returns from trading them are much greater.
This indicates that the relationship between pair volatility, tick spacing, and fees should be as follows: for volatile pairs with a high risk of impermanent loss, both tick spacing and fees should be higher, while for more stable pairs with a low risk of impermanent loss, both can be lower.
It is up to the user to decide which pairs are more stable or volatile. What the protocol defines is the relationship between tick spacing and fee tier.
The Uniswap V3 factory contract provides some default values, but Uniswap governance can add additional tick-spacing-fee pairs. This is the subject of the next section.
Fee and tick spacing in the code
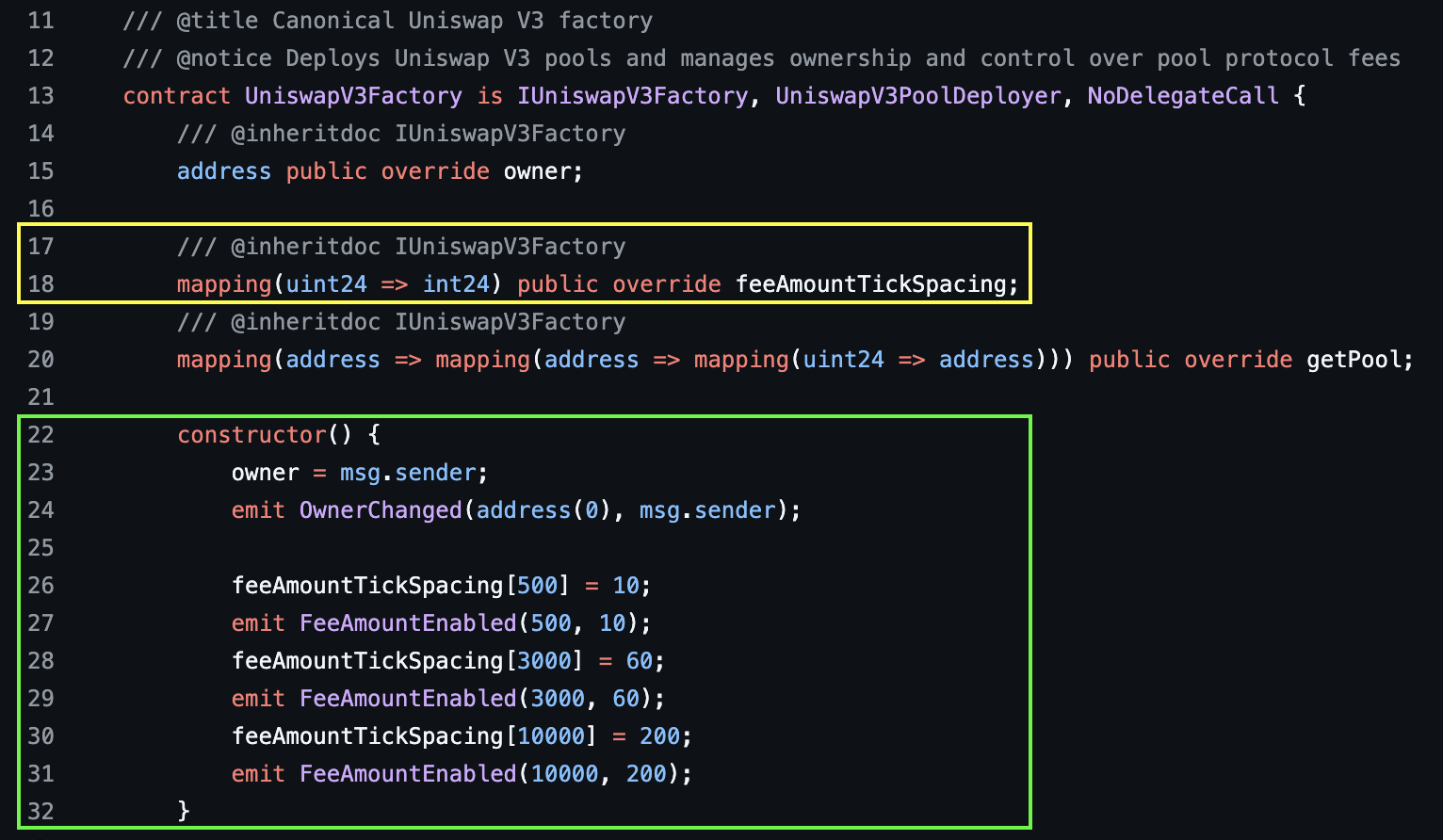
The relationship between fee and tick spacing is contained in the mapping feeAmountTickSpacing (yellow box in the figure below) in the UniswapV3Factory.sol contract. The factory contract is responsible for creating new pools.
The initial relationship between fee and tick spacing was defined during the deployment of the Factory contract, as shown in the constructor in the image below (green box).
The current relationship between fee and tick spacing is shown in the following table. There is no strict “mathematical” relationship between the fee and tick spacing. It’s up to protocol governance to decide the optimal fee for a given tick spacing.
| fee tier | fee tier (basis points) | tick spacing |
|---|---|---|
| 0.01% | 1 | 1 |
| 0.05% | 5 | 10 |
| 0.3% | 30 | 60 |
| 1% | 100 | 200 |
As we can see, a fee of 0.01% corresponds to a tick spacing of 1, while a fee of 0.3% corresponds to a tick spacing of 60.
Basis points
Fees are measured in basis points. One basis point is 1/100th of 1 percent, or 0.01%. For example, 5 basis points is 5 * 0.01%, or 0.05%.
Fee tiers can be updated
The mapping from fee to tick spacing can be updated using the function enableFeeAmount, which can only be called by governance.
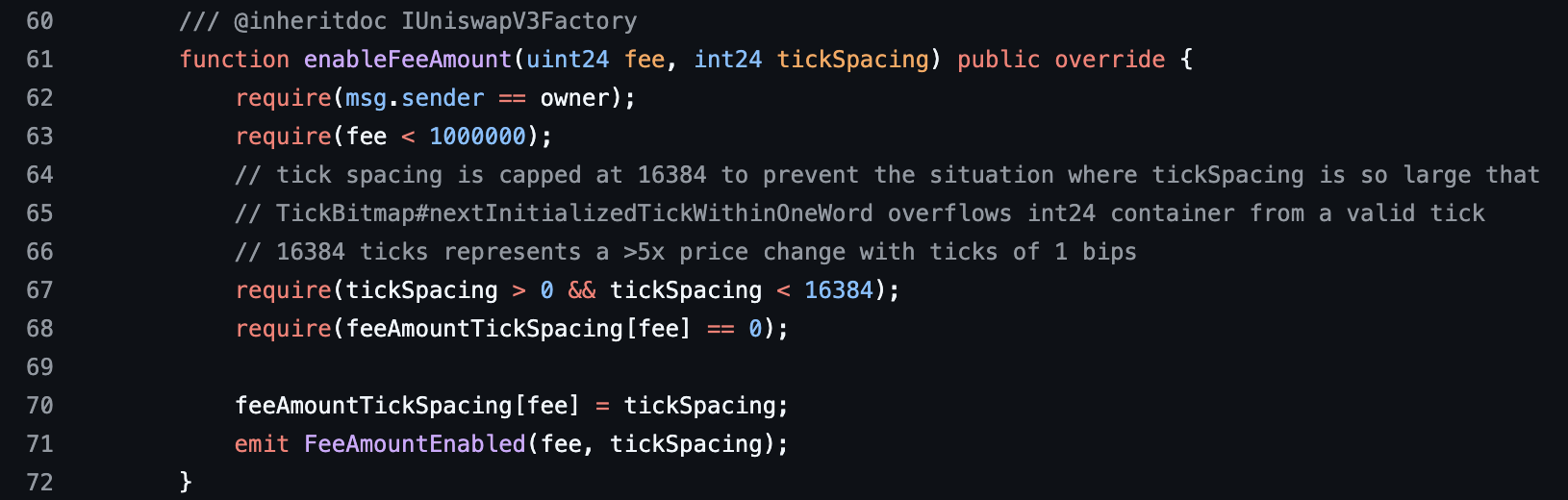
The 1 basis point tier (the 0.01% fee) is not in the constructor, but Uniswap governance added the 1 basis point fee tier on March 5, 2022. You can see the transaction on the tally dashboard.
The available fee tiers can vary on different chains. For example, on the L2 Base, fee tiers for 2, 3, and 4 basis points are available. This addition was executed by governance on September 16, 2024.
Creating a new pool using the factory contract
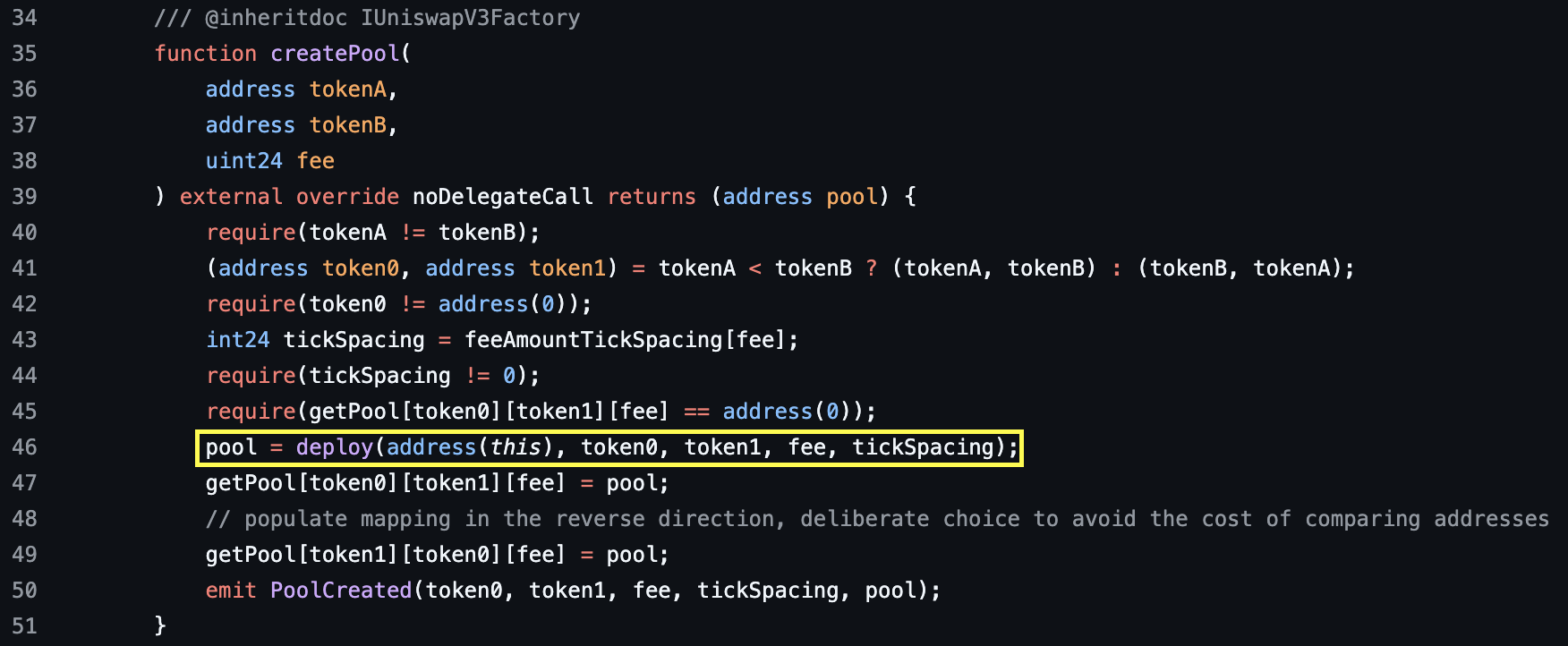
To create a new pool, a user must pass in the addresses of both tokens and the desired fee tier. The tick spacing is then calculated from the feeAmountTickSpacing mapping.
A pool is uniquely defined by these three parameters. Thus, it is possible to create pools with the same token pair but different fee tiers. In this case, the market determines which of these pools becomes the ‘popular’ one.
The deployment of the pool by the factory contract
When the pool is deployed by the factory contract, it is passed both the fee and the tickSpacing and these are set as public immutable variables.
Note that there are no restrictions on who can call createPool — it is permissionless as long as the pool for that token pair and fee tier hasn’t been created yet.
Both of these immutable variables (fee and tickSpacing) are public in UniswapV3Pool.sol. In fact, all of the arguments passed to the pool’s constructor are stored in public immutable variables:
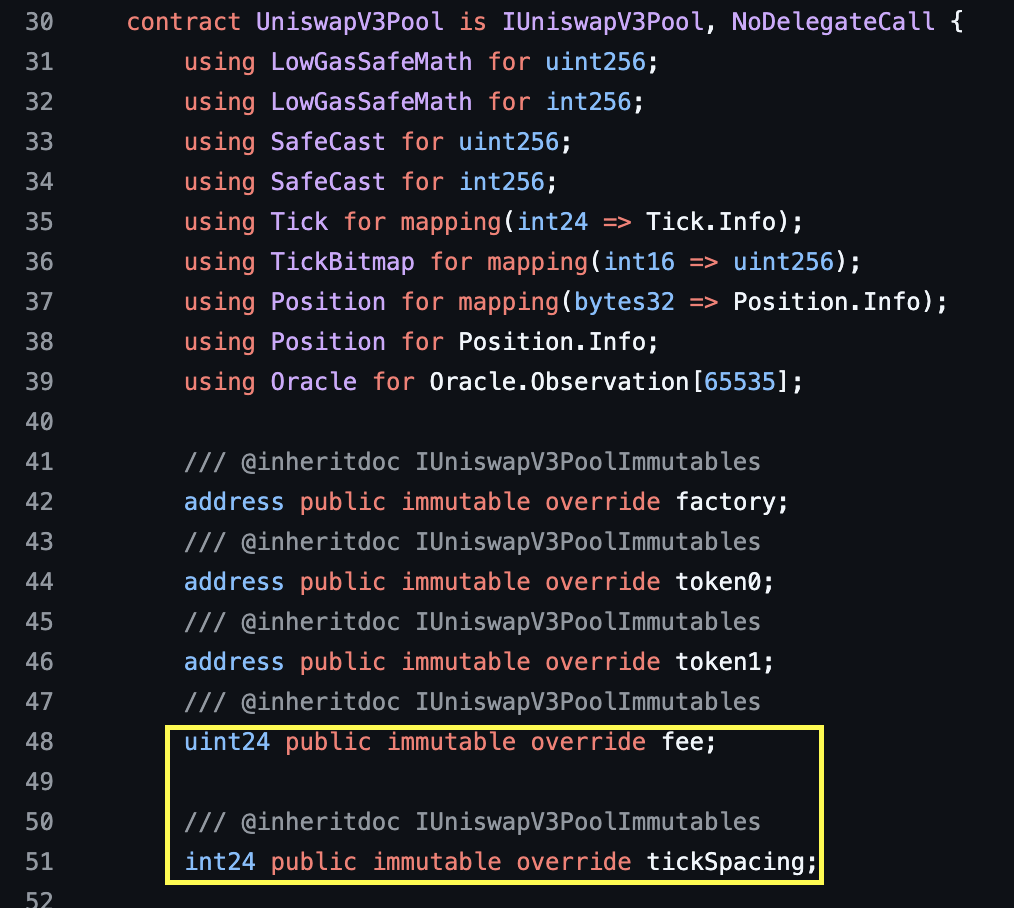
Examples
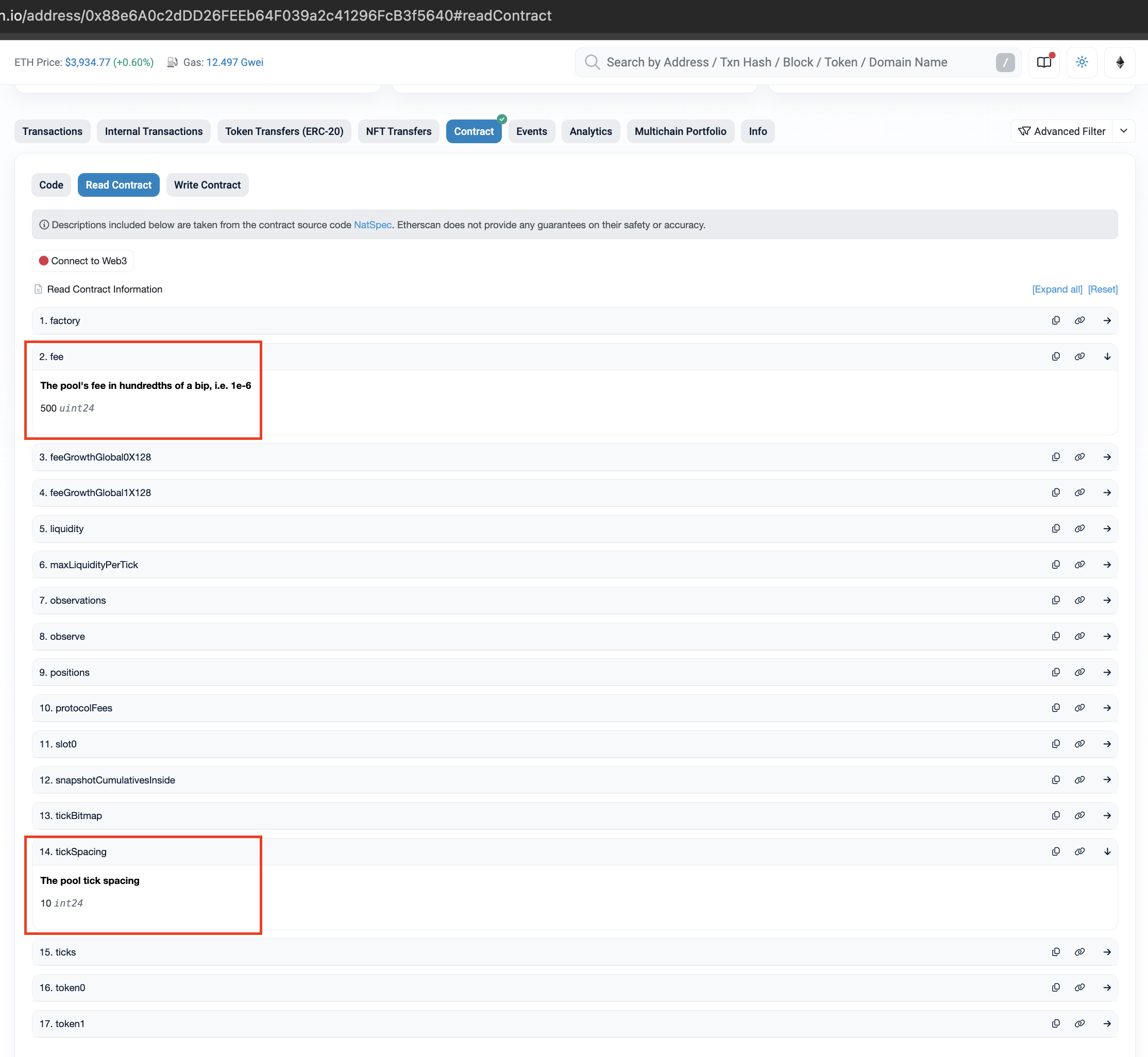
Let’s use the USDC/ETH Pool as a running example. We can see the fee is 5 basis points and it has a tick spacing of 10:
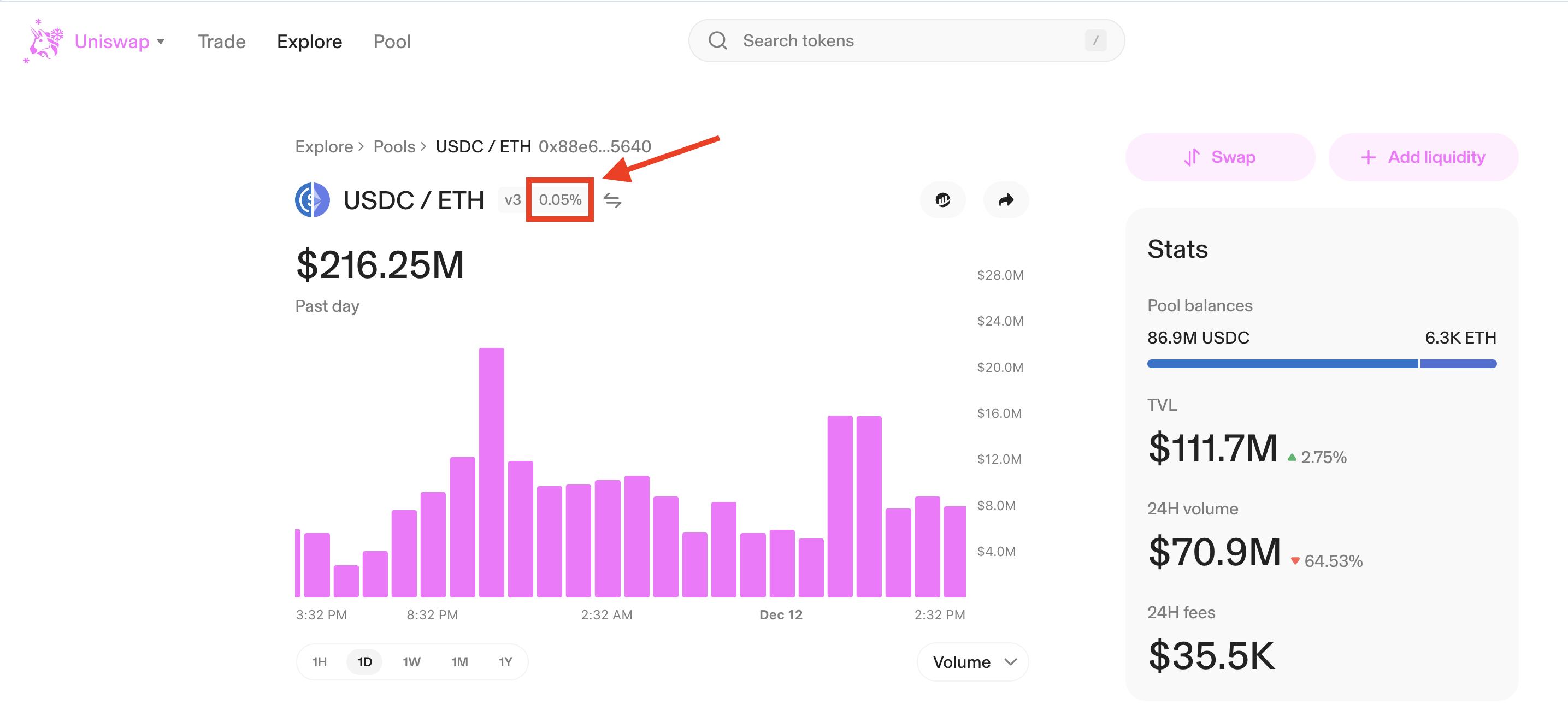
This is how the frontend for that pool knows the fee tier is 0.05%.
Summary
- Not all ticks in a pool can be used—only those that are multiples of the tick spacing are allowed.
- The relationship between tick spacing and fees is set in a mapping in the Factory. Governance can add more tick spacing and fee options.
- Frequent tick crossing results in higher gas costs, as we will learn when studying swaps. Therefore, pools with higher price volatility and/or lower liquidity should use larger tick spacing to minimize the frequency of allowed ticks being crossed.
- On the other hand, for pools with lower price volatility and/or highly liquid pairs, tick spacing can be smaller, as liquidity providers will have a clearer idea of where to concentrate their liquidity.
Practice Exercises
Look through the Uniswap V3 Pools.
- What is the tick spacing for USDC/USDT on mainnet? Since there might be multiple pools with the same pair but different fee, look for the pool that has at least a million dollars in volume in the last day.
- What is the tick spacing for a pair that holds a memecoin?