Square and Multiply Algorithm

The square and multiply algorithm computes integer exponents in $\mathcal{O}(\log n)$ (logarithmic time). The naive way to compute an exponent $x^n$ is to multiply $x$ by itself, $n$ times, which would require $\mathcal{O}(n)$ time to compute.

Suppose we want to compute $x^{20}$. Instead of multiplying $x$ with itself 20 times, we start with $x$ and repeatedly square it until we compute $x^{16}$:

$$ \begin{align*} x^2&=x\cdot x\\ x^4&=x^2\cdot x^2\\ x^8&=x^4\cdot x^4\\ x^{16}&=x^8\cdot x^8 \end{align*} $$

Observe that we can compute $x^{20}$ as:

$$ x^{20}=x^4x^{16} $$

The fact that the exponents “add” in this manner is called the product-of-powers rule in algebra.

This article is part of a series on the Uniswap V3 codebase. Uniswap V3 uses the square and multiply algorithm for converting a tick index to a square root price. However, this article is also for anyone wanting to learn how the square and multiply algorithm works.

Squared exponents sequence

We will use the term “squared-exponents sequence” multiple times in this article, which is $x^1,x^2,x^4,x^8,\dots$. Each term is a square of the previous. The base $x$ can have any non-zero value. For example, \$0.7^1,0.7^2,0.7^4,…$ is a valid squared-exponents sequence. Similarly, $-1.56,-1.56^2,…,-1.56^{32},-1.56^{64}$ is also a valid squared-exponents sequence.

Square and multiply with a fractional base

If we know in advance that the base will be a fixed value, and that the exponents we might potentially compute have a known upper-bound, then we can precompute the squared-exponents sequence and then do lookups instead of multiplication. For example, if we want to compute \$0.7^x$ and we know in advance that $x$ won’t be larger than 63, we can precompute the following values:

$$ \begin{align*} &0.7\\ &0.7^2=0.49\\ &0.7^4=0.2401\\ &0.7^8=0.05764801\\ &0.7^{16}=0.00332329\\ &0.7^{32}=0.00001104 \end{align*} $$

Then, for example, if we want to compute \$0.7^{44}$, we can multiply the appropriate precomputed values from the squared exponent sequence together as follows:

$$ \begin{align*} 0.7^{44}&=0.7^{32}\times0.7^{8}\times0.7^{4}\\ 0.00000015&=0.00001104\times0.05764801\times0.2401 \end{align*} $$

The reader is encouraged to redo \$0.7^{44}$ on their calculator to double-check this.

When we cache values in this manner, we must know in advance the upper bound of the exponent our application must handle.

Square and Multiply Algorithm with Fractional Exponents

Suppose instead of computing \$0.7^x$ we want to compute $\sqrt[3]{0.7^x}$? This is equivalent to \$0.7^{x/3}$. We can still use the square-and-multiply algorithm because the exponent is divided by a constant number, so the product of powers rule still applies. In other words,

$$ 0.7^{44/3}=0.7^{32/3}\times0.7^{8/3}\times0.7^{4/3} $$

To compute \$0.7^{44/3}$, we would change the powers of $0.7$ we precompute as follows:

$$ \begin{align*} &0.7^{1/3}=0.8879040017426006\\ &0.7^{2/3}=0.7883735163105242\\ &0.7^{4/3}=0.6215328012198205\\ &0.7^{8/3}=0.38630302299215685\\ &0.7^{16/3}=0.14923002557287887\\ &0.7^{32/3}=0.02226960053248208 \end{align*} $$

Then, to compute \$0.7^{44/3}$ we multiply the precomputed exponents as follows:

$$ \begin{align*} 0.7^{44/3}&=0.7^{32/3}\times0.7^{8/3}\times0.7^{4/3}\\ 0.005346931087848946&=0.02226960053248208\times0.38630302299215685\times0.6215328012198205 \end{align*} $$

Again, the reader is encouraged to redo these calculations themselves.

Picking the elements from the squared exponent sequence

If want to compute $b^{44}$ How do we figure out which powers of $b$ we need from our squared-exponents sequence? In other words, how do we quickly determine we need $b^{32}, b^{8}, b^{4}$ and not $b^{32}, b^{4}, b^{1}$ ?

Given a target sum, such as 44, how do we quickly determine that 32, 8, and 4 are the sums? Alternatively, suppose we are trying to compute $b^{37}$. The elements of the squared exponent sequence we need are $b^{32},b^{4},b^{1}$ — how do we quickly determine we need $b^{32},b^{4},b^{1}$ and not $b^{2},b^{8},b^{16}$?

A naïve approach would be to do a linear search from the largest precomputed exponent downwards and subtract the largest one that does not overshoot the target. For example, if we were computing $5^{44}$, that means we have already computed the squared exponent sequence of 5. We scan downwards and find that 32 is the closest value to 44. Then we scan down again to find 16, but note that adding 32+16 overshoots 44, so we skip 16 and move on to 8, and so on.

Using the binary representation to extract the sum components

Instead of using the above-mentioned linear search, we can be more efficient by observing that the binary representation of the target exponent tells us precisely which elements to use from the squared exponent sequence.

This is best illustrated by examples.

To convert a binary number to a decimal number, we use the following formula where $b_i$ is the $i$-th bit in the binary number:

$$ \text{decimal\_value}=2^{n-1}b_{n-1}\dots+8b_3+4b_2+2b_1+b_0=\sum_{i=0}^{n-1}2^ib_i $$

The binary value of 13 is 1101 because

$$ \begin{align*} 44=8&\cdot1 \\ +4&\cdot1 \\ +2&\cdot0 \\ +1&\cdot1 \end{align*} $$

The binary value of 52 is 110100 because

$$ \begin{align*} 52 = 32&\cdot1\\ +16&\cdot1\\ +8&\cdot0\\ +4&\cdot1\\ +2&\cdot0\\ +1&\cdot0 \end{align*} $$

Therefore, if we want to compute $b^{13}$, and our squared exponent sequence is $b^8,b^4,b^2,b^1$, then we can look at the binary representation of 1011 and determine that we should pick the 8 exponent, the 4 exponent, and the 1 exponent, then compute

$$ b^{13}=b^8\cdot b^4\cdot b^1 $$

since

$$ 13=8+4+1 $$

Thus, we can quickly determine that 13 can be written as 8 + 4 + 1 since the 3rd bit, 2nd bit, and 0th bit are 1.

Detecting if a bit is set

We can detect if the n-th bit is 1 in a binary representation with the following logic:

function nthBitSet(uint256 x, uint8 n) public pure returns (bool isSet) {

    isSet = x & uint256(2)**n != 0;
}

Consider the binary representation of powers-of-two:

uint256(2)**n creates a number with only the nth bit set to 1. For example, if n = 3, this would produce the binary value 1000. $2^3=8$ and 1000 is the binary representation of 8, as shown in the Table above. If the bitwise AND of x and 2^n is not zero, then isSet is true.

How Bitwise AND Works

Bitwise AND returns 1 only if both corresponding bits are 1; otherwise, it returns 0. For example, 8 & 13 = 8 because the binary representation of 8 is 1000 and the binary representation of 13 is:

$$ \begin{aligned}13 &= 1 \cdot 2^3 \\ &+ 1 \cdot 2^2 \\ &+ 0 \cdot 2^1 \\ &+ 1 \cdot 2^0\end{aligned} $$

or 1101. When we bitwise AND 1000 with 1101 we get 1000 since both 8 and 13 have a common 1-bit in the 3rd position.

This is illustrated below:

Suppose x = 13 (binary: 1101) and n = 3:

x           = 1101 (decimal 13)
2**n        = 1000 (decimal 8)
------------------------------
bitwise AND = 1000 (decimal 8) != 0, thus true.

Thus, nthBitSet(13, 3) returns true.

Since the final result 1000 is not equal to zero, then we know that there had to have been an overlapping of 1 bits between x and 2^n — this indicates that bit must be equal to one.

Example 2: Is the 1st bit set in 13? We can create a “mask” for the first bit as 2**1 as shown below:

Suppose x = 13 (binary: 1101) and n = 1:

x           = 1101 (decimal 13)
2**n        = 0010 (decimal 2)
------------------------------
bitwise AND = 0000 (decimal 0) == 0, thus false.

Thus, nthBitSet(13, 1) returns false.

Since the final result is 0000, we know the 1st bit is not set.

Example 3: Is the 0th bit set in 13?

Suppose x = 13 (binary: 1101) and n = 0:

x           = 1101 (decimal 13)
2**n        = 0001 (decimal 1)
------------------------------
bitwise AND = 0001 (decimal 1) == 1, thus true.

Thus, nthBitSet(13, 0) returns true.

Python example of \$0.7^x$

We now combine everything we’ve learned to produce the following function, which raises 0.7 to a power up to 32:

pow1 = 0.7
pow2 = 0.48999999999999994 # 0.7^2
pow4 = 0.24009999999999995 # 0.7^4
pow8 = 0.05764800999999997 # 0.7^8
pow16 = 0.0033232930569600965 # 0.7^16

def raise_07_to_p(p):
    # computes 0.7^p
    assert p < 32

    # if p = 0, we return 1, which is correct
    # since 0.7^0 = 1
    accumulator = 1

    if p & 1 != 0:
        accumulator = accumulator * pow1
    if p & 2 != 0:
        accumulator = accumulator * pow2
    if p & 4 != 0:
        accumulator = accumulator * pow4
    if p & 8 != 0:
        accumulator = accumulator * pow8
    if p & 16 != 0:
        accumulator = accumulator * pow16

    return accumulator

# check correctness
print(0.7**14, raise_07_to_p(14))
print(0.7**18, raise_07_to_p(18))
print(0.7**30, raise_07_to_p(30))

The above code avoids repetitive multiplication by using only the powers of 0.7 that correspond to 1s in the binary representation of the exponent.

So far, we have used regular/floating-point numbers. However, in real-world systems like smart contracts, we often use fixed-point numbers (or Q-numbers).

Using the square and multiply algorithm with fixed-point numbers

After multiplying fixed-point numbers (or Q-numbers) together, the result must be “normalized,” i.e., the result needs to be divided by the scaling factor. For example, when we multiply two 18-decimal fixed-point numbers together, we need to divide the result by $10^{18}$, otherwise the final result will be written with 36 decimals.

Python and Solidity implementation of precomputed square and multiply — with fixed-point numbers

We will first implement the square and multiply algorithm in Python, then translate that code to Solidity. The Solidity version will use fixed-point numbers as Solidity does not have floating points. Below, we use Python to calculate the powers of 0.7 as 128-bit fixed point Q numbers as a reference implementation:

from decimal import *
import math
getcontext().prec = 100

for i in [1,2,4,8,16,32]:
    print(f"0.7^{i} * 2**128 =", math.floor(Decimal(0.7) ** Decimal(i) * Decimal(2**128)))

When we run the code above, we get the following constants

(base) ➜ python sqmul.py
0.7^1 * 2**128 = 238197656844656909312789480019373064192
0.7^2 * 2**128 = 166738359791259825940851714385556537344
0.7^4 * 2**128 = 81701796297717304344478436853479174360
0.7^8 * 2**128 = 19616601291081919795097291374069314602
0.7^16 * 2**128 = 1130858027394302849221997646234907220
0.7^32 * 2**128 = 3758172630847077410107089115980415

Solidity implementation of square and multiply

The Solidity implementation below uses 128-bit fixed-point numbers, meaning there are 128 bits after the number, or equivalently, the fractional number is scaled up by multiplying by $2^{128}$. The >> 128 operation is equivalent to dividing by $2^{128}$.

contract SquareAndMultiply {

    // z7_x means 0.7^x
    uint256 constant z7_1 = 238197656844656909312789480019373064192;
    uint256 constant z7_2 = 166738359791259825940851714385556537344;
    uint256 constant z7_4 = 81701796297717304344478436853479174360;
    uint256 constant z7_8 = 19616601291081919795097291374069314602;
    uint256 constant z7_16 = 1130858027394302849221997646234907220;
    uint256 constant z7_32 = 3758172630847077410107089115980415;

    function powZ7(uint256 e) public pure returns (uint256) {
        require(e < 64, "e too large");

        // if e is zero, return 1 as a 128-bit fixed point number
        uint256 acc = 1 << 128;

                // powers of 2 are written in hex, 0x10 = 16 and 0x20 = 32
        if (e & 0x1 != 0) acc = (acc * z7_1) >> 128;
        if (e & 0x2 != 0) acc = (acc * z7_2) >> 128;
        if (e & 0x4 != 0) acc = (acc * z7_4) >> 128;
        if (e & 0x8 != 0) acc = (acc * z7_8) >> 128;
        if (e & 0x10 != 0) acc = (acc * z7_16) >> 128;
        if (e & 0x20 != 0) acc = (acc * z7_32) >> 128;

        // check the answer by doing acc / 2**128
        // in a language that has floating points
        // then check that equals 0.7^e
        return acc;
    }
}

Why not just use an exponent opcode?

When raising an integer to an integer power, it’s generally more efficient to use a virtual machine’s built-in opcode.

However, this opcode doesn’t include the normalization step described above. Therefore, if at least one of $b$ or $x$ in $b^x$ is a fixed-point number, then we cannot use the virtual machine’s exp opcode.

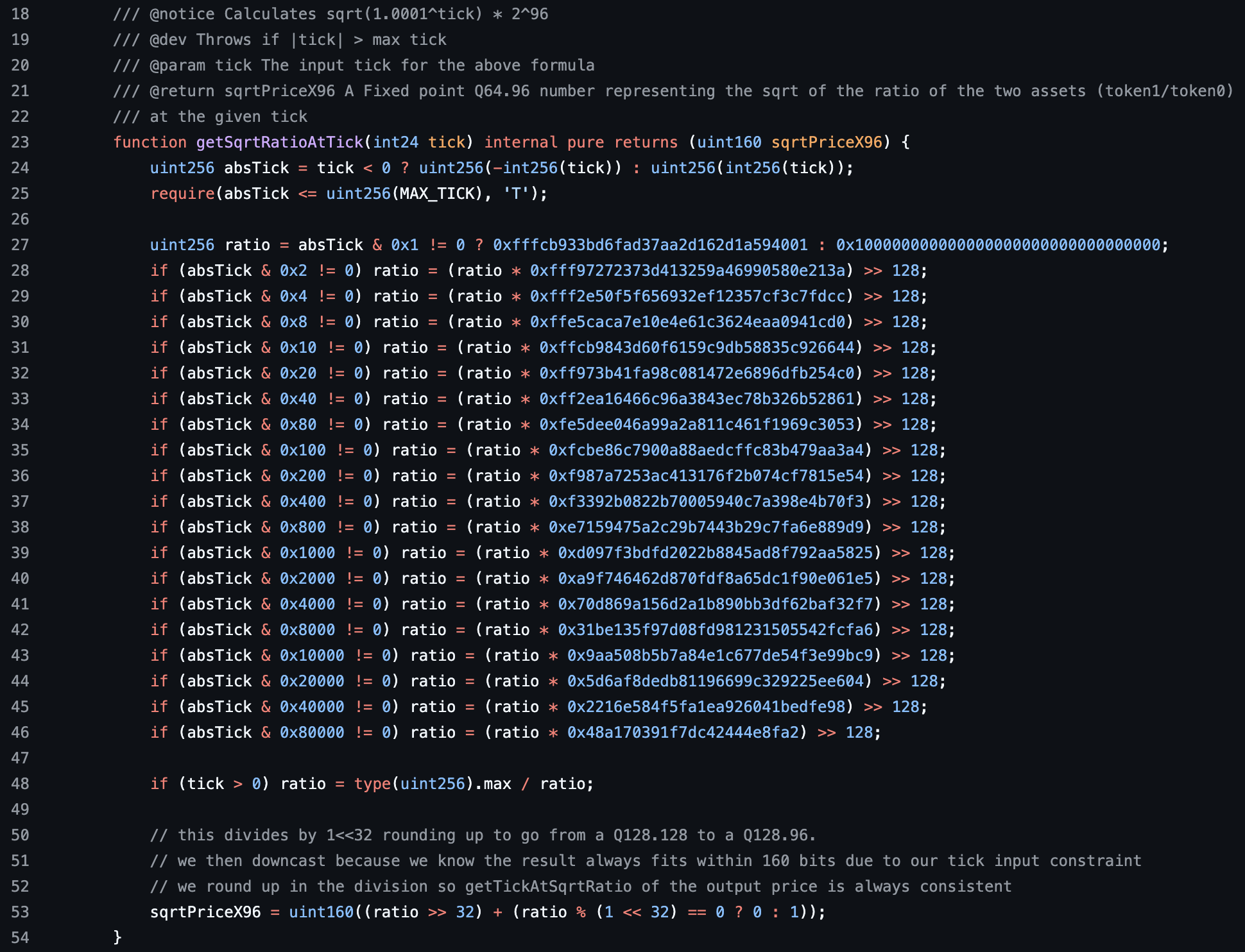
Square and multiply in Uniswap V3

To convert a tick to a square root price, Uniswap V3 must compute

$$ \texttt{sqrtPrice}=\sqrt{1.0001^\text{i}} $$

(with some corrections for sqrtPrice being a Q64.96 number). Since

1. the base is fixed and the only variable is the exponent and

2. the range of ticks is known in advance. Uniswap V3 can (and does) use the Square and Multiply Algorithm. This is explained in the next chapter.

As a teaser, here is a screenshot of getSqrtRatioAtTick() from the Uniswap V3 Tickmath Library. This should look very similar to the Solidity code we wrote above. At a high level, the function checks if a bit in absTick is set, and if it is, it multiplies ratio by a precomputed power of 1.0001.