Uniswap V2 was designed to collect 1/6th of the swap fees to the protocol. Since a swap fee is 0.3%, 1/6th of that is 0.05%, so 0.05% of every trade would go to the protocol.
Although this feature was never actually activated, we discuss this feature anyway since some forks may use it. It is also very easy to get the calculation wrong, so investing the time now to understand it will help you catch errors in similar calculations later.
Prerequisites
You need to be familiar with all the prior chapters in the Uniswap V2 Book to be able to follow along.
Collecting protocol fees during swaps is inefficient
It would be inefficient to collect 0.05% of the fee on every trade because that would require additional token transfers. Transferring ERC20 tokens requires a storage update, so transferring to two addresses instead of one would be considerably more expensive.
Therefore, the fee is collected when a liquidity provider calls burn or mint. Since these operations are infrequent compared to swapping tokens, this will lead to gas savings. To collect the mintFee, the contract calculates the amount of fees collected since that last happened, and mints enough LP tokens to the beneficiary address such that the beneficiary is entitled to 1/6th of the fee.
Terminology of fee and mintFee
To avoid confusion in terminology, we refer to "fee" as the 0.3% collected from traders during the swap, and the "mintFee" the 1/6th of the 0.3% fee. Yes, having fee in both terms is not great nomenclature, but that’s what we have to work with.
Liquidity is the square root of the products of the token balances in the pool. The justification for this formula was discussed in the Uniswap V2 swap function article. Some literature refers to this as √𝑘 where 𝑘 = 𝑥𝑦 and 𝑥 and 𝑦 are the token balances. We refer to liquidity with ℓ to minimize notation.
Computing the mintFee assumptions
For this to work, Uniswap V2 relies on the following two invariants:
If mint and burn are not called, the liquidity of the pool can only increase.
The increase in liquidity is purely due to fees (or donations).
By measuring the increase in liquidity since the last mint or burn, the pool knows how much fees were collected.
These would be good invariant tests to write, but for now we will take for granted that they are true.
Example calculation of mintFee
Suppose at t₁ the pool starts at 10 token0 and 10 token1.
After a lot of trading and fee collection, the new pool balance is 40 token0 and 40 token1 at t₂.
Liquidity is measured as the square root of the product of the two tokens, i.e. liquidity = sqrt(xy). The liquidity was 10 at t₁ and 40 at t₂, sqrt(100) and sqrt(1600) respectively. We are going to charge a fee on the growth from 10 to 40.
Specifically, 3/4ths, or 30 units of liquidity of the pool is due to fees. We want to mint enough LP tokens, the “mintFee” such that the beneficiary receives 1/6th of the “fee portion” of the pool. That is, they should be entitled to 5 units of liquidity (30 / 6).
Remember, the mint fee is dilutive. We mint more such that the proportional ownership of the liquidity providers is reduced.
How do we compute this in general?
Let’s use the following notation:
The key insight is the invariant
That is, if the mintFee η can redeem the amount of liquidity due to the protocol 𝑝, then the original LP supply 𝑠 can redeem the rest of the pool 𝑑.
The graphic below solves for η in terms of the change in liquidity.
With that derivation in mind, the bulk of the Uniswap V2 _mintFee function should be self-explanatory. Here are some changes in notation:
current liquidity after fees ℓ₂ is rootK
previous liquidity is kLast
the supply of LP tokens before dilution s is totalSupply
the function is state changing, it mints the mintFee inside the function rather than return the calculation of the mintFee (blue highlight)
the fee can be switched on an off with the flag feeOn which we haven’t discussed yet
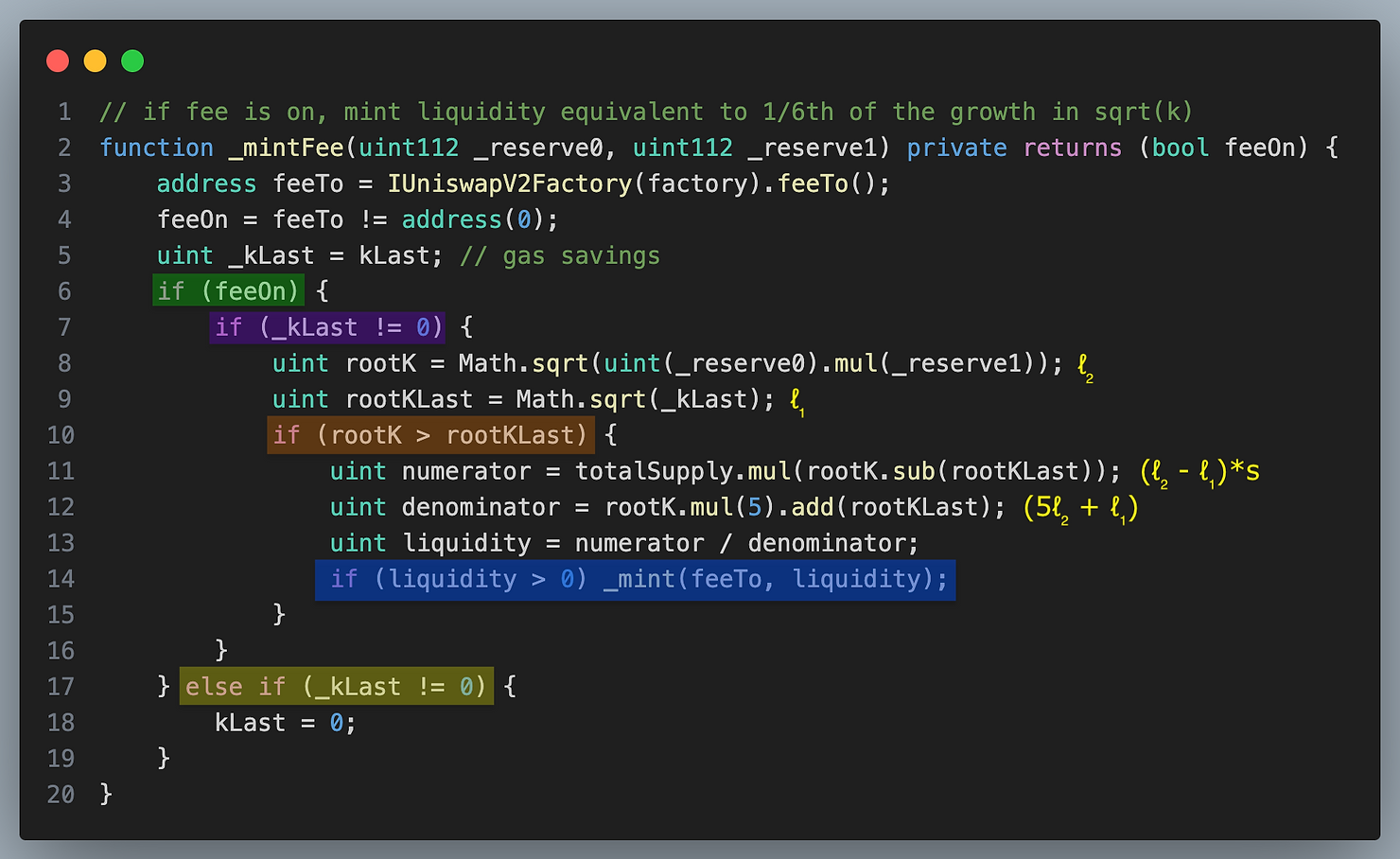
We will dive into this function some more, but first we want to note where kLast gets updated.
Where klast gets updated
In the code above, kLast is not set unless feeOn is switched to false. It is set at the completion of mint and burn but not swap because we are interested in measuring the growth of fees due to swaps between liquidity deposit and withdrawal events. The places kLast is set is marked with a yellow box.
Mint function
Burn function
The feeOn Switch
Now that we understand how kLast is updated, we can fully explain the _mintFee function.
Let’s consider the possibilities in the code snippet above, repeated for convenience.
The feeOn is false, nothing is minted (green highlight)
The feeOn is false, kLast is zero (yellow highlight)
The feeOn is false, kLast is not zero (yellow highlight)
The feeOn is true, but there was no growth in liquidity (orange highlight)
The feeOn is true, and there was liquidity growth (orange highlight), so the mint fee applies (blue highlight)
It’s easier to see the logic in a decision tree, so here is the decision tree with the branches colored the same as the if statements.
Learn more with RareSkills
Please see our blockchain bootcamp to see our course offerings.