Uniswap V2: Calculating the Settlement Price of an AMM Swap

This article explains how to determine the price settlement of a trading pair in an Automated Market Maker (AMM). It answers the question of “How many token X can be swapped for token Y from the AMM?”.

The swap() function on Uniswap V2 requires you to pre-calculate the amount of tokens to swap from the pool (including 0.3% in trading fees).

Consider an ETH / USDC trading pair with 100 ETH and 100 USDC in the Liquidity Pool. For simplicity, this assumes 1 ETH is 1 USDC.

Although the spot price of 1 ETH is 1 USDC and vice versa, this does not mean we can trade 25 USDC for 25 ETH as this will not preserve the constant product formula.

Authorship

This article was co-authored by Aymeric Taylor (LinkedIn, Twitter), a research intern at RareSkills.

The Constant Product formula theory: x * y ≥ k

The constant product formula dictates that in a pair pool of token X and token Y, the product of the two asset quantities in the pool (X times Y) at all times should remain constant at the very least.

$$x \times y \geq k$$

The constant product formula ensures an inverse relationship between the two tokens, modeling market supply and demand. As one token quantity increases (deposited into the AMM), the other should decrease (withdrawn from the AMM contract).

The inverse relationship is more clearly shown if we reorder the variables as in the equation below.

$$y \geq \frac{k}{x}$$

Let’s plot our running example into the constant formula equation:

• x-axis = 100 ETH
• y-axis = 100 USDC
• k = 10,000 (100 ETH * 100 USDC)
• The Pink Line depicts the curve *x y ≥ 10,000**

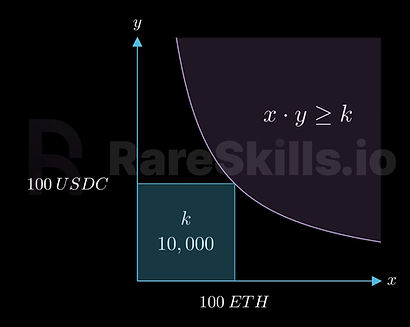
The boxed area under the curve is the constant k, product of x and y.

We’ll soon demonstrate how we can swap ETH for USDC in a way that preserves this constant.

Uniswap constant product formula implementation

In practice, the constant product formula is implemented through comparing the constant product of the liquidity pool before and after the trade to ensure it remains at least constant.

$$k_\text{before} \leq k_\text{after}$$

Uniswap does not stop you from giving the AMM more than you should, in the case that you do, it is your fault for underestimating how much you can withdraw, hence the ≤ sign.

Expanding the equation above, we get the equivalent equation below:

$$\underbrace{x_\text{Before} \times y_\text{Before}}_{k_\text{Before}} \leq \underbrace{x_\text{After} \times y_\text{After}}_{k_\text{After}}$$

• x_Before and y_Before is the quantity of each tokens in the pool before the swap.
• x_After and y_After is the quantity of tokens in the pool after the swap.

This means that the constant product of the pool after swapping ETH for USDC has to at least stay the same.

$$\underbrace{\text{ETH}_\text{Before} \times \text{USDC}_\text{Before}}_{k_\text{Before}} \leq \underbrace{\text{ETH}_\text{After} \times \text{USDC}_\text{After}}_{k_\text{After}}$$

Uniswap V2 imposes a 0.3% AMM trading fee for every swap. When factoring in the fees, the constant product of the liquidity pool increases with each swap. This growth in the pool is the key incentives for liquidity providers. Only when liquidity providers withdraw their liquidity would the constant product of the pool decrease. We will show you how to calculate the swap with trading fees included towards the end of this article.

Why we cannot swap 25 ETH for 25 USDC

To determine if a swap is valid or not, we need to pre-calculate how the swap would affect the constant product of the pool. Does it remain at least the same?

We’ll denote ΔETH & ΔUSDC as the amount swapped into and out of the liquidity pool respectively.

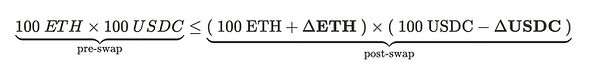
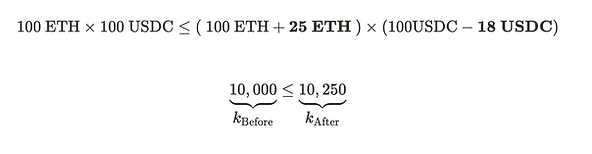
Swapping 25 ETH for 25 USDC would mean that we deposit 25 ETH into the AMM, and withdraw 25 USDC from it. This would adjust the pool’s liquidity to 125 ETH and 75 USDC. The AMM will reject this swap since the constant product of the pool decreases post swap

The post-swap product is short of the pre-swap product, 10,000, which violates the constant product invariant. The graph below visualizes this swap.

Clearly, we cannot expect to withdraw 25 USDC — we will have to withdraw less to preserve the constant product invariant.

Determining the Correct USDC Swap Amount

Circling back to the previous example, adding 25 ETH to the pool increases the ETH quantity to 125 ETH (100 + 25). The next task is to find the new, decreased quantity of USDC in the pool that preserves the constant product, thereby ensuring the AMM would accept it.

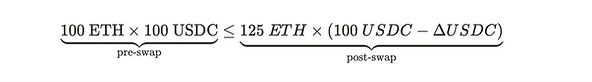
We have an equation that reveals the maximum value of ΔUSDC that can be swapped for 25 ETH.

Solving for ΔUSDC

We rearrange the equation to solve for ΔUSDC explicitly.

The pool now has 125 ETH and 80 USDC, which amounts to a constant product of 10,000.

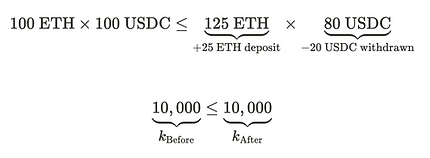
Swapping 25 ETH for 20 USDC is the most amount of USDC you can extract from the AMM liquidity pool. This swap is accepted since it preserves the constant product formula. 20 USDC is one-fifth less than 25 USDC, hence we experienced slippage during this swap. Slippage is the degree to which the price moves as a result of our trade. If we placed a smaller trade, the price we end up paying would be close to 1 USDC : 1 ETH. But because our trade is large, we end up paying a higher price for less USDC, thus incurring a higher slippage.

We can visualize this swap below.

The generalized formula for calculating the swap can be expressed as follows:

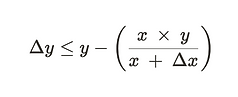
• x and y represents the quantity of tokens in the liquidity pool before the swap
• Δx represents the amount of token deposited into the AMM
• Δy represents the amount swapped out of the AMM

Miscalculating the swap: Giving the AMM more than you should

If you take out less, for example 18 USDC, the AMM would still accept it since the constant product in the liquidity pool increases, but you are at a loss since you did not maximize your swap.

Calculating the swap with fees

The calculations we performed above were “theoretical” which excluded trading fees. As mentioned before, Uniswap V2 applies a 0.3% trading fee for every swap, but the fees only apply towards the token deposited into the AMM. Say we swapped token X for token Y, 0.3% fee is taken out only from X, and not from Y.

How Uniswap V2 calculates the 0.3% fee is by dividing the deposited token into 2 parts:

• Fee: 0.3%
• Amount available left for the swap: 99.7%

For 25 ETH, our fee and the amount available left for the swap would be:

• Fee(0.3%): 0.075 ETH
• Amount available left for the swap(99.7%): 24.925 ETH

The fee is immediately excluded from this swap’s calculation, so the swapper will not be credited with the 0.3% fee portion.

What’s left is the amount available for the swap which is 24.925 ETH. This is the actual amount that we are swapping USDC for from the pool.

Let’s solve for the maximum amount of USDC (ΔUSDC) we can withdraw out of the pool. Adding 24.925 ETH to the pool would increase the ETH quantity to 124.925 ETH.

solving for ΔUSDC we get:

Accounting for the 0.3% swapping fee, we could withdraw approximately 19.952 USDC from the AMM. This is less than the 20 USDC we could receive in the example with no fees.

The primary difference in calculation when factoring in fees is that we multiply the deposited token by 99.7%, 0.3% is set aside and allocated to the AMM. Given Δx is the deposited token and Δy is the withdrawn token amount, the general equation becomes:

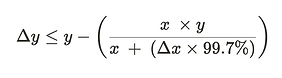
Learn more with RareSkills

This article is part of our advanced Solidity Bootcamp. Please see the curriculum to learn more.

Originally Published April 17, 2024