If we have a Pedersen vector commitment $A$ which contains a commitment to a vector $\mathbf{a}$ as $A = a_1G_1 + a_2G_2+\dots + a_nG_n$ we can prove we know the opening by sending $\mathbf{a}$ to the verifier who would check that $A \stackrel{?}= a_1G_1 + \dots + a_nG_n$. This requires sending $n$ elements to the verifier (assuming $\mathbf{a}$ is of length $n$).
In the previous chapter, we showed how to do this with zero knowledge. In this chapter, we show how to prove knowledge of an opening while sending less than $n$ elements, but without the zero knowledge property.
The technique we develop here will be an important building block for proving a valid computation of an inner product with a proof of size $\log n$ where $n$ is the length of the vectors.
In the previous chapter, we showed how to prove we executed the inner product correctly, but without revealing the vectors or the result. However, the proof is of size $\mathcal{O}(n)$ because of the step where the prover sends $\mathbf{l}_u$ and $\mathbf{r}_u$.
The subroutine in this article will be important for reducing the size of the proof. This article isn’t concerned with zero knowledge because the previously discussed algorithm has the zero knowledge property. That is $\mathbf{l}_u$ and $\mathbf{r}_u$ weren’t secret to begin with, so there is no need to obfuscate them.
Given an agreed upon basis vector $\mathbf{G}=[G_1,\dots,G_n]$ the prover gives the verifier a Pedersen vector commitment $A$, where $A$ is a non-blinding commitment to $\mathbf{a}$, i.e. $A = \langle[a_1,\dots,a_n],[G_1,\dots,G_n]\rangle$ and wishes to prove they know the opening to the commitment while sending less than $n$ terms, i.e. sending the entire vector $[a_1,\dots,a_n]$.
Shrinking the proof size relies on three insights:
The first insight we will leverage is that the inner product is the diagonal of the outer product. In other words, the outer product “contains” the inner product in a sense. The outer product, in the context of 1D vectors, is a 2D matrix formed by multiplying every element in the first 1D vector with every other element in the second vector. For example:
$$ \begin{align*} \mathbf{a}=[a_1, a_2],\space \mathbf{b}=[b_1, b_2], \end{align*} \space\space \mathbf{a} \otimes \mathbf{b} = \begin{pmatrix} \boxed{a_1 b_1} & a_1 b_2 \\ a_2 b_1 & \boxed{a_2 b_2} \\ \end{pmatrix} $$
This might seem like a step in the wrong direction because the outer product requires $\mathcal{O}(n^2)$ steps to compute. However, the following insight shows it is possible to indirectly compute the outer product in $\mathcal{O}(1)$ time.
A second observation is that the sum of the terms of the outer product equals the product of the sum of the vectors. That is,
$$ \sum_{i=1}^{n} a_i\sum_{i=1}^{n} b_i=\sum\mathbf{a} \otimes \mathbf{b} $$
For our example of vectors $[a_1,a_2]$ and $[b_1,b_2]$ this would be
$$ \underbrace{(a_1 + a_2)(b_1 + b_2)}_{\sum a_i\sum b_i} = \underbrace{a_1b_1 + a_1b_2 + a_2b_1 + a_2b_2}_{\sum\mathbf{a} \otimes \mathbf{b}} $$
Graphically, this can be visualized as the area of the rectangle with dimensions $(a_1 + a_2) \times (b_1 + b_2)$ having the same “area” as $a_1 \times b_1 + a_1 \times b_2 + a_2 \times b_1 + a_2 \times b_2$
$$ \begin{array}{|c|cc|} \hline &a_1+a_2\\ \hline b_1&a_1b_1 + a_1b_2\\ +b_2& + a_2b_1 + a_2b_2\\ \hline \end{array}= \begin{array}{|c|c|c|} \hline &a_1&a_2\\ \hline b_1&a_1b_1&a_2b_1\\ \hline b_2&a_1b_2&a_2b_2\\ \hline \end{array} $$
In our case, the $\mathbf{b}$ vector is actually the basis vector of elliptic curve points, so we are saying that
$$ (a_1 + a_2)(G_1 + G_2) = a_1G_1 + a_1G_2 + a_2G_1 + a_2G_2 $$
Note that our original Pedersen commitment
$$ A = \langle[a_1,a_2],[G_1,G_2]\rangle = a_1G_1 + a_2G_2 $$
is embedded in the boxed terms of the outer product:
$$ (a_1 + a_2)(G_1 + G_2) = \boxed{a_1G_1} + a_1G_2 + a_2G_1 + \boxed{a_2G_2} $$
Therefore, by multiplying the sums of the vector entries together, we also compute the sum of outer product.
Since the inner product is the diagonal of the outer product, we have indirectly computed the inner product by multiplying the sums of the vector entries together. To prove that we know the inner product, we need to prove we also know the terms of the outer product that are not part of the inner product.
For vectors of length $2$, let’s call the parts of the outer product that are not part of the inner product the off-diagonal product.
Below, we mark the terms that make up the off-diagonal product with $\square$ and the terms that make up the inner product with $\blacksquare$:
$$ \begin{array}{|c|c|c|} \hline &a_1&a_2\\ \hline b_1&\blacksquare&\square\\ \hline b_2&\square&\blacksquare\\ \hline \end{array} $$
We can now formally state the identity we will rely on going forward. If $n=2$ then: $$\sum\mathbf{a}\otimes\mathbf{b}=\langle\mathbf{a},\mathbf{b}\rangle+\mathsf{off\_diagonal}(\mathbf{a},\mathbf{b})$$
The identity also holds if one of the vectors is a vector of elliptic curve points (even if their discrete logs are unknown).
For cases where $n > 2$, proving knowledge of an inner product means the prover needs to convince the verifier they know the “area” of the purple-shaded region below.
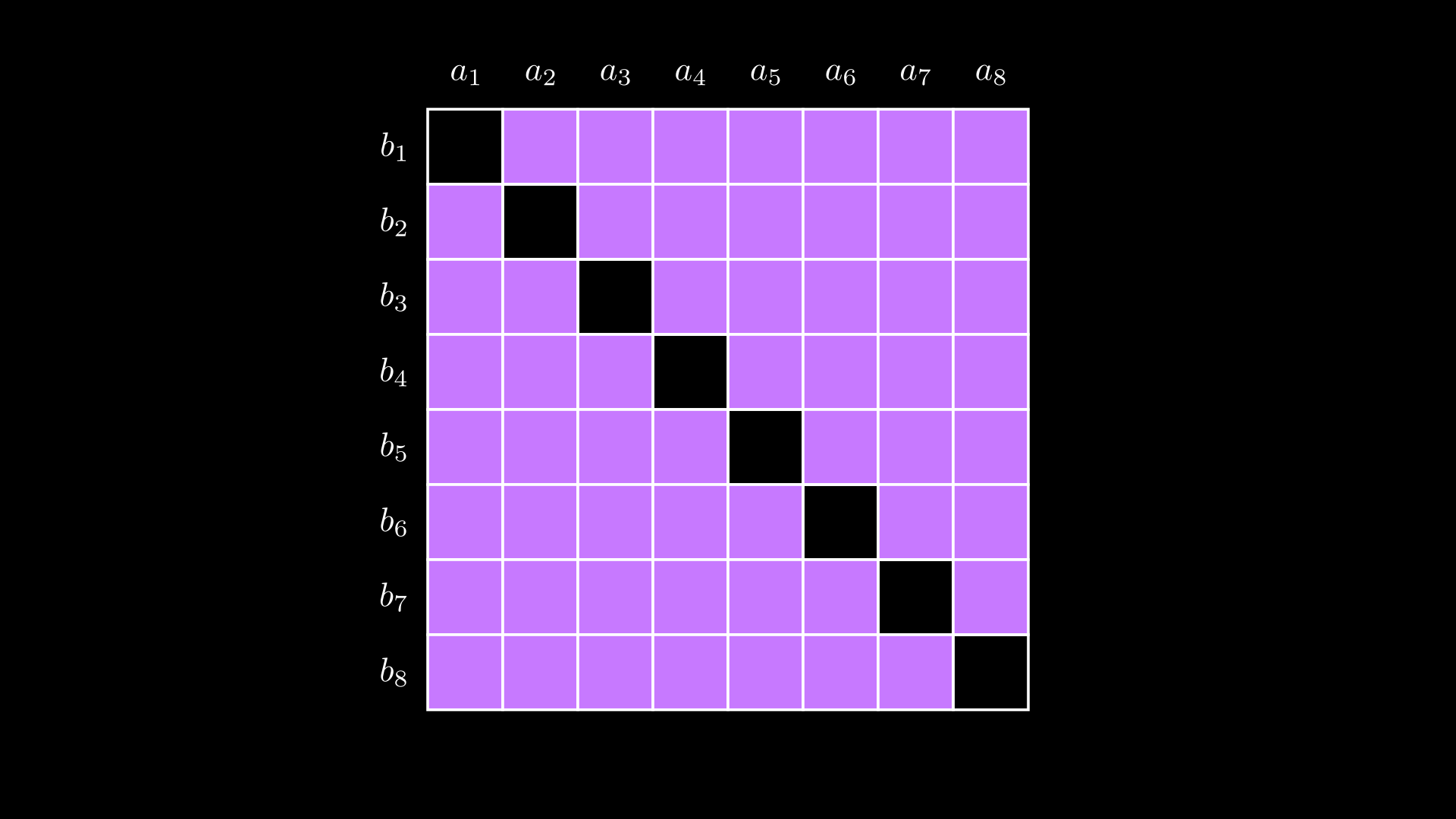
Conveying this information succinctly when $n > 2$ is trickier, so we will revisit this later.
In the case of $n = 2$, the area is simply the off-diagonals.
An important corner case is where we have a vector of length $1$. In that case, the prover simply sends the verifier $\mathbf{a}$ (which is of length $1$) and the verifier simply multiplies the single element of $\mathbf{a}$ with the single element of $\mathbf{G}$.
We can now create a first draft of an algorithm for the case $n=2$ that proves we have computed the inner product of $\mathbf{a}$ and $\mathbf{G}$, which is equivalent to showing we know the commitment $A$.
The interaction between the prover and the verifier is as follows:
Graphically, $L$ and $R$ can be seen as follows:
$$ \begin{array}{|c|c|c|} \hline &a_1&a_2\\ \hline G_1&&R\\ \hline G_2&L&\\ \hline \end{array} $$
$$\underbrace{a’G’}_\text{outer product sum} = \underbrace{A}_\text{inner product} + \underbrace{L + R}_\text{off-diagonal terms}$$
In expanded form, the above equation is: $$\underbrace{(a_1+a_2)(G_1+G_2)}_\text{outer product} = \underbrace{a_1G_1 + a_2G_2}_\text{inner product} + \underbrace{a_1G_2 + a_2G_1}_\text{off-diagonal terms}$$
Note that the check above is equivalent to the identity from earlier:
$$\sum\mathbf{a}\otimes\mathbf{G}=\langle\mathbf{a},\mathbf{G}\rangle+\mathsf{off\_diagonal}(\mathbf{a},\mathbf{G})$$
However, there is security issue — the prover can find multiple proofs for the same commitment. For example, the prover could chose $L$ randomly, then compute
$$ R = a’G’ – L $$
To prevent this, we re-use a similar idea from our discussion of zero knowledge multiplication — the prover must include verifier-provided randomness $u$ in their computation. They must also send $L$ and $R$ in advance of getting $u$ so $L$ and $R$ cannot be “advantageously” selected.
The reason the prover must send $L$ and $R$ individually, instead of the sum $L + R$ is that the prover is able to hack the protocol by moving value between $L$ and $R$ with no restriction. That is, since
$$L + R = a’G’$$
the prover could pick some elliptic curve point $S$ and compute a fraudulent $L’$ and $R’$ as
$$\underbrace{(L + S)}_{L’} + \underbrace{(R – S)}_{R’} = a’G’$$
We need to force the prover to keep $L$ and $R$ separate.
Here is the updated algorithm that corrects this bug:
The prover and verifier agree on a basis vector $[G_1, G_2]$ where the points are chosen randomly and their discrete logs are unknown.
The prover computes and sends to the verifier $(A, L, R)$: $$ \begin{align*} A &= a_1G_1 + a_2G_2 && \text{// vector commitment we are proving knowledge of}\\ L &= a_1G_2 && \text{// left diagonal term}\\ R &= a_2G_1 && \text{// right diagonal term}\\ \end{align*} $$
The verifier responds with a random scalar $u$.
The prover computes and sends $a’$:
$$a’ = a_1 + a_2u$$
Under the hood this is: $$ \underbrace{a_1G_2}_L + \underbrace{u(a_1G_1 + a_2G_2)}_{uA} + \underbrace{a_2u G_1}_{u^2R} = \underbrace{(a_1 + u a_2)}_{a’}(u G_1 + G_2) $$
which is identically correct if the prover correctly computed $a’$, $L$, and $R$.
Note that the verifier applied $u$ to $G_2$ whereas the prover applied $u$ to $a_1$. This causes the terms of the original inner product to be the linear coefficients of the resulting polynomial.
The fact that $L$ and $R$ are separated by $u^2$, which the verifier controls, prevents a malicious prover from doing the attack described earlier. That is, the prover cannot shift value from $R$ to $L$ because the value they shift must be scaled by $u^2$, but the prover must send $L$ and $R$ before they receive $u$.
The verifier is only carrying out a single multiplication, $a’$ times $(uG_1 + G_2)$. Even though we started with vectors of length $2$, the verifier only carries out $n/2=1$ point multiplications.
The operation $a_1 + a_2u$ turned a vector $\mathbf{a}$ of length $2$ into a vector of length $1$. Hence, the prover and verifier are both jointly constructing a new vector of length $1$ given the prover’s vectors and the verifier’s randomness $u$.
Since they have both compressed the original vector to a vector of length $1$, the verifier can use the identity $\langle\mathbf{a}’,\mathbf{G}’\rangle=\mathbf{a}’\otimes\mathbf{G}’$ when $n = 1$. Here, $\mathbf{a}’ = a_1 + a_2u$ and $\mathbf{G’} = G_1u + G_2$.
As a quick summary of the algorithm,
$$L + uA + u^2R \stackrel{?}= a'(uG_1 + G_2)$$
Now let’s see why the prover cannot cheat.
The only “degree of freedom” the prover has on step 3 is $a’$.
To come up with an $a’$ that satisfies
$$L + uA + u^2R = a'(uG_1 + G_2)$$
the prover needs to know the discrete logs of $G_1$ and $G_2$. Specifically, they would have to solve
$$a’=\frac{l + ua + u^2r}{ug_1 + g_2}$$
where
However, the prover does not know the discrete logs $g_1$ and $g_2$, so they cannot compute $a’$.
There are only two values valid for $a’$ that satisfy $L + uA + u^2R = a'(uG_1 + G_2)$. Note that the equation $L + uA + u^2R$ forms a quadratic polynomial with respect to variable $u$ and $a'(uG_1+G_2)$ forms a linear polynomial. By the Schwartz-Zippel Lemma, the equation has at most two solutions. As long as the order of the field is $\gg 2$, then the probability of the prover finding $a’$ such that it results in an intersection point of $L + uA + u^2R = a'(uG_1 + G_2)$ is negligible.
Instead of combining $a_1$ and $a_2$ together as $a_1 + a_2u$, the prover combines them as $a’ = a_1u + a_2u^{-1}$ and the verifier does $G’ = u^{-1}G_1 + u G_2$. Note that the powers of the two vectors are applied in the opposite order. When we compute the outer product, the inner product terms will have the $uu^{-1}$ cancel:
$$ [a_1u, u^{-1}a_2] \otimes [u^{-1}G_1, uG_2]= \begin{array}{|c| c c|} \hline & ua_1 & u^{-1}a_2 \\ \hline G_1u^{-1} & \color{green}{a_1G_1} & a_1G_2u^2 \\ G_2u & a_2G_1u^{-2} & \color{green}{a_2G_2} \\ \hline \end{array} $$
Arguably, this approach is “cleaner” so we will use that going forward.
The computation $a_1x + a_2x^{-1}$ happens so frequently in Bulletproofs that it is handy to give it a name, which we call $\mathsf{fold}(\mathbf{a},x)$. The first argument $\mathbf{a}$ is the vector we are folding (which must be of even length, if not we pad it with a $0$). Fold splits the vector $\mathbf{a}$ of length $n$ into $n/2$ pairs, and returns a vector of length $n/2$ as follows:
$$\mathsf{fold}(\mathbf{a}, x)=[a_1x+a_2x^{-1},a_3x+a_4x^{-1},\dots,a_{n-1}x+a_nx^{-1}]$$
If we do $\mathsf{fold}(\mathbf{a},x^{-1})$ we mean:
$$\mathsf{fold}(\mathbf{a}, x^{-1})=[a_1x^{-1}+a_2x,a_3x^{-1}+a_4x,\dots,a_{n-1}x^{-1}+a_nx]$$
When $n=2$, $\mathsf{fold}(\mathbf{a},x)$ is simply $a_1x+a_2x^{-1}$ and $\mathsf{fold}(\mathbf{a},x^{-1})=a_1x^{-1}+a_2x$.
We now restate the algorithm using the Bulletproofs paper’s approach to randomness:
Assuming the prover was honest, the final check under the hood expands to:
$$ \begin{align*} (a_1G_2)u^2 + (a_1G_1 + a_2G_2) + u^{-2}(a_2G_1) &= (a_1u + a_2u^{-1})(u^{-1} G_1 + uG_2)\\ (a_1G_2)u^2 + (a_1G_1 + a_2G_2) + u^{-2}(a_2G_1) &=a_1G_1+a_1u^2G_2+a_2u^{-2}G_1+a_2G_2\\ a_1u^2G_2 + a_1G_1 + a_2G_2 + a_2u^{-2}G_1 &=a_1G_1+a_1u^2G_2+a_2u^{-2}G_1+a_2G_2\\ a_1G_1 + a_1u^2G_2 + a_2u^{-2}G_1 + a_2G_2 &=a_1G_1+a_1u^2G_2+a_2u^{-2}G_1+a_2G_2\\ \end{align*} $$
Assuming array $\mathbf{a}$ has even length (if not, we can add a zero element to make it even length), we can pairwise-partition the array. Below is an example of a pairwise-partition:
$$\mathbf{a} = [a_1, a_2, a_3, a_4, a_5, a_6, a_7, a_8]=[a_1, a_2] [a_3, a_4] [a_5, a_6] [a_7, a_8]$$
Similarly, we can pair-wise partition $\mathbf{G}$.
$$\mathbf{G} = [G_1, G_2, G_3, G_4, G_5, G_6, G_7, G_8]=[G_1, G_2] [G_3, G_4] [G_5, G_6] [G_7, G_8]$$
Each of the sub-pairs can then be treated as instances of computing the inner product using the $n=2$ case from earlier:
We could then prove we know the four $n=2$ commitments $a_1G_1 + a_2G_2$, $a_3G_3 + a_4G_4$, $a_5G_5 + a_6G_6$, and $a_7G_7 + a_8G_8$ and this would be equivalent to proving we know the opening to the original commitment.
However, that would create four extra $(L, R)$ terms for pairs we are proving — i.e. no efficiency gain in terms of the size of the data the prover transmits.
The naive solution would be for the prover to commit and send:
$$\begin{align*} A_1 &= a_1G_1+a_2G_2\\ A_2 &= a_3G_3+a_4G_4\\ A_3 &= a_5G_5+a_6G_6\\ A_4 &= a_7G_7+a_8G_8\\ L_1 &= a_1G_2\\ R_1 &= a_2G_1\\ L_2 &= a_3G_4\\ R_2 &= a_4G_3\\ L_3 &= a_5G_6\\ R_3 &= a_6G_5\\ L_4 &= a_7G_8\\ R_4 &= a_8G_7\\ \end{align*}$$
Graphically, that can be seen as follows: \begin{array}{c|c|} &a_1 & a_2 & a_3 & a_4 & a_5 & a_6 & a_7 & a_8\\ \hline G_1&&R_1\\ \hline G_2&L_1\\ \hline G_3&&&&R_2\\ \hline G_4&&&L_2\\ \hline G_5&&&&&&R_3\\ \hline G_6&&&&&L_3\\ \hline G_7&&&&&&&&R_4\\ \hline G_8&&&&&&&L_4\\ \hline \end{array}$$As a (key!) optimization, we add up all the $A_i$, $L_i$ and $R_i$ terms from each of the pairs to become the single points $A$, $L$, $R$. In other words, the prover only sends:$$\begin{align*} A &= A_1 + A_2 + A_3 + A_4\\ L &= L_1 + L_2 + L_3 + L_4\\ R &= R_1 + R_2 + R_3 + R_4\\ \end{align*}$$The operation described is shown in the animation below:### Security of adding all the commitments and off-diagonals together An initial concern with such an optimization is that since the prover is adding more terms together, there is more opportunity to hide a dishonest computation.We now show that once the prover sends $A$ (and $L$ and $R$) they can only create one unique proof that they know the opening to $A$.Observe that $L$ is computed as $L = a_1G_2 + a_3G_4 +a_5G_6+a_7G_8$ and $R$ is computed as $R = a_2G_1 + a_4G_3 +a_6G_5+a_8G_7$. They do not have any common elliptic curve points. Thus, the prover cannot “shift value” from $L$ to $R$ because they do not know the discrete logs of any of the points. Effectively, $L$ is a Pedersen vector commitment of $[a_2, a_4, a_6, a_8]$ to the basis vector $[G_1, G_3, G_5, G_7]$. The security assumption of a Pedersen vector commitment is that the prover can only produce one possible vector opening. “Shifting values around” after they send the commitment would mean the prover can compute a different vector other than $[a_2, a_4, a_6, a_8]$ which produces the same commitment. But that contradicts our assumption that a prover can only produce a single valid vector for a Pedersen commitment. A similar argument can be made for $R$.$A$ is the addition of four Pedersen commitments (the commitments to the vectors $[a_1, a_2]$, $[a_3, a_4]$, $[a_5, a_6]$, $[a_7, a_8]$). However, the fact that several Pedersen commitments are added together is immaterial from a security perspective. It makes no difference if the commitments are computed separately and then added, or $A$ is computed as a vector of $n = 8$. Consider that:$$\begin{align*} &\space a_1G_1 + a_2G_2\space + \space a_3G_3 + a_4G_4\space\space + \space\space a_5G_5 + a_6G_6\space + \space a_7G_7 + a_8G_8\\ =&(a_1G_1 + a_2G_2) + (a_3G_3 + a_4G_4) + (a_5G_5 + a_6G_6) + (a_7G_7 + a_8G_8)\end{align*}$$
For example, the prover might “shift value” from $a_1G_1$ to $a_2G_1$.
The only remaining concern is that the prover could shift value from $a_1G_1$ in $A$ to $a_2G_1$ in $L$ since they share a common elliptic curve point. However, this is prevented by the random $u$ from the verifier as shown previously.
Hence, once the prover sends $(A, L, R)$ computed in the manner described in this section, they can only create one possible opening, and thus create only one possible proof.
We leave it as an exercise for the reader to work out an example to check that the final verification check is algebraically identical if the prover was honest. We suggest using a small example such as $n=4$.
$P$ is a commitment to the original vector $\mathbf{a}$ with respect to the basis vector $\mathbf{G}$. $L$ is a commitment to the vector made up of the left off-diagonals of the pairwise outer products and $R$ is a commitment to the components of the right off-diagonals of the pairwise outer products.
The sum $Lu^2 + P + Ru^{-2}$ is itself a vector commitment of the vector $\mathsf{fold}(\mathbf{a},u)$ to the basis $\mathsf{fold}(\mathbf{G}, u^{-1})$, which has size $n/2$.
We show the relationship graphically below:
To prove we know the opening to a commitment of size $n/2$, we can simply send the vector of size $n/2$, which in this case is $\mathsf{fold}(\mathbf{a},u)$.
Using this interpretation, the algorithm is doing the following:
Because the verifier needs to compute $\mathsf{fold}(\mathbf{G}, u^{-1})$, this will require iterating over the entire $\mathbf{G}$ vector, which will take $\mathcal{O}(n)$ time. Although the proof size can be smaller than the original vectors, verifing the proof will still take linear time.
We have shown how the prover can show they know an opening to a Pedersen vector commitment $A$ while sending only $n/2$ elements ($\mathbf{a}$ folded).
In the next chapter, we show how to recursively apply this algorithm so that the prover only sends $\mathcal{O}(\log n)$ elements.
Exercise: Implement the algorithm described in this chapter. Use the following code as a starting point:
from py_ecc.bn128 import G1, multiply, add, FQ, eq, Z1
from py_ecc.bn128 import curve_order as p
import numpy as np
from functools import reduce
import random
def random_element():
return random.randint(0, p)
def add_points(*points):
return reduce(add, points, Z1)
# if points = G1, G2, G3, G4 and scalars = a,b,c,d vector_commit returns
# aG1 + bG2 + cG3 + dG4
def vector_commit(points, scalars):
return reduce(add, [multiply(P, i) for P, i in zip(points, scalars)], Z1)
# these EC points have unknown discrete logs:
G_vec = [(FQ(6286155310766333871795042970372566906087502116590250812133967451320632869759), FQ(2167390362195738854837661032213065766665495464946848931705307210578191331138)),
(FQ(6981010364086016896956769942642952706715308592529989685498391604818592148727), FQ(8391728260743032188974275148610213338920590040698592463908691408719331517047)),
(FQ(15884001095869889564203381122824453959747209506336645297496580404216889561240), FQ(14397810633193722880623034635043699457129665948506123809325193598213289127838)),
(FQ(6756792584920245352684519836070422133746350830019496743562729072905353421352), FQ(3439606165356845334365677247963536173939840949797525638557303009070611741415))]
# return a folded vector of length n/2 for scalars
def fold(scalar_vec, u):
pass
# your code here
# return a folded vector of length n/2 for points
def fold_points(point_vec, u):
pass
# your code here
# return L, R as a tuple
def compute_secondary_diagonal(G_vec, a):
pass
# your code here
a = [9,45,23,42]
# prover commits
A = vector_commit(G_vec, a)
L, R = compute_secondary_diagonal(G_vec, a)
# verifier computes randomness
u = random_element()
# prover computes fold(a)
aprime = fold(a, u)
# verifier computes fold(G)
Gprime = fold_points(G_vec, pow(u, -1, p))
# verification check
assert eq(vector_commit(Gprime, aprime), add_points(multiply(L, pow(u, 2, p)), A, multiply(R, pow(u, -2, p)))), "invalid proof"
assert len(Gprime) == len(a) // 2 and len(aprime) == len(a) // 2, "proof must be size n/2"
Range Proof A range proof in the context of inner product arguments is a proof that the scalar $v$ has been committed to $V$ and $v$ is less than $2^n$ for some non-negative integer $n$. This article shows how the Bulletproofs paper constructs such a proof. The high level idea is that if we can […]
Reducing the number of equality checks (constraints) through random linear combinations Random linear combinations are a common trick in zero knowledge proof algorithms to enable $m$ equality checks to be probabilistically checked with a single equality check. Suppose we have $m$ inner products we are trying to prove. Instead of creating $m$ proofs, we create […]
Inner Product Algebra In this article, we give some useful algebraic tricks for inner products that will be useful in deriving range proofs (and encoding circuits as inner products) later. Each rule will be accompanied by a simple proof. Notation Variables in bold, like $\mathbf{a}$,denote a vector. Variables not in bold, like $v$, denote a […]
Bulletproofs ZKP: Zero Knowledge and Succinct Proofs for Inner Products Bulletproofs ZKPs allow a prover to prove knowledge of an inner product with a logarithmic-sized proof. Bulletproofs do not require a trusted setup. In the previous chapters, we showed how to prove knowledge of an inner product without revealing the vectors or the inner product, […]